minimum stream power to uniquely define channel stability. An optional use of
the analytical method is to assign a value for slope, thereby obtaining unique
solutions for width and depth. Typically there will be two solutions for each
slope.
Meander Geometry
Input
The purpose of the meander calculations is to provide both curvilinear and
Cartesian coordinates for a meander planform based on the sine-generated curve.
The sine-generated curve has been shown to effectively replicate meander
patterns in a wide variety of natural rivers. (Langbein and Leopold, 1966)
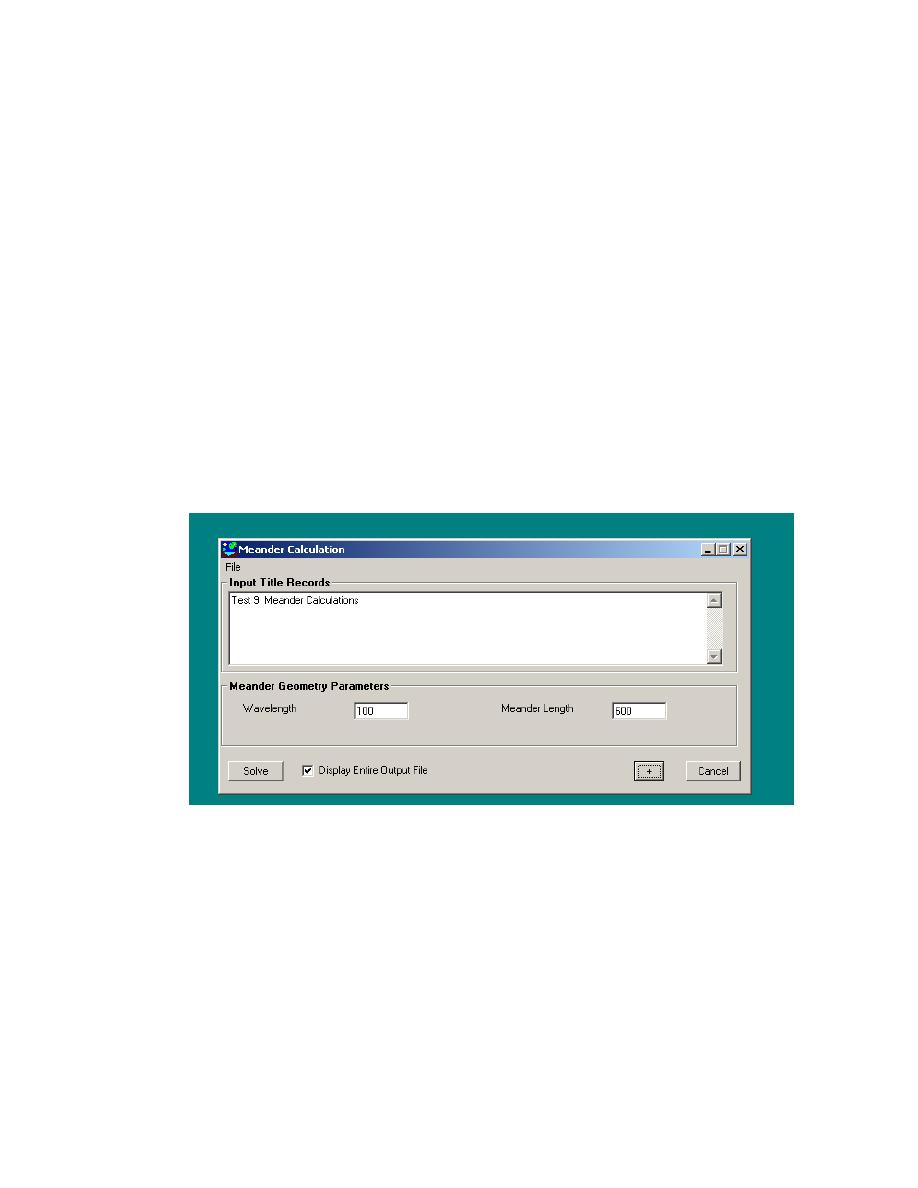
Required input are the meander arc length and the meander wavelength, as
shown in Figure 6.20. Title records are optional. The Meander arc length is the
actual length of the channel, whereas the wavelength is the length, along the
valley, of one full meander.
Figure 6.20. The Meander Calculation screen, with input.
Output
The output file first displays the SAM.hyd banner and echoes the input. An
internal banner stresses that these calculations are appropriate for sand-be
streams. The input wavelength and meander length are then printed along with
the sinuosity, maximum deflection angle (in degrees), and the amplitude. Then a
table of "Coordinates along one meander wavelength" is printed, giving the
distance along the channel, deflection angle in degrees, the Y perpendicular to
the valley slope, and the X along the valley slope.
121
Chapter 6
Input Requirements and Program Output for SAM.hyd




 Previous Page
Previous Page
