1
exp a cos(θ - θ p )
D(θ) =
(C3)
2πI0 (a)
where I0 is the modified Bessel function of the first kind and a is a parameter
describing the degree of directional spreading with a → ∞ representing a
unidirectional wave field.
Wrapped-Normal Spreading Function
The wrapped-normal distribution was suggested by Mardia (1972) and is
given by:
1
1 N
1
+ ∑ exp - ( jσθ )2 cos j(θ - θ p )
D(θ) =
(C4)
2π
π j =1
2
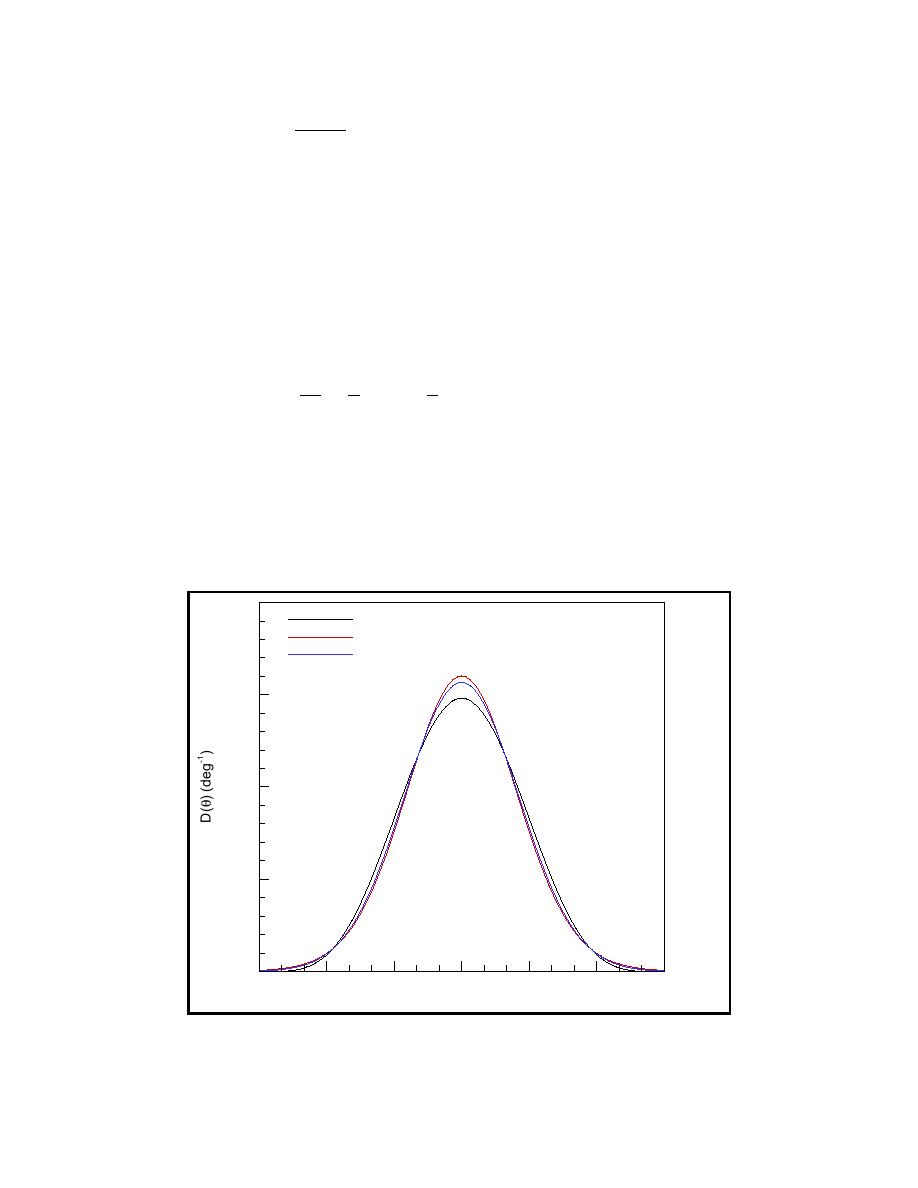
Figure C1 shows a plot of the distributions for the three different spreading func-
tion formulations corresponding to a standard deviation σθ of 25.5 deg. The
associated spreading indices are s = 2 for the cosine-power function and a = 5.55
for the circular-normal distribution. Thirty components (N = 30) were used for the
wrapped-normal distribution. The cosine-normal and wrapped-normal distribu-
tions are slightly narrower than the cosine-power function although the differences
can be considered to be minimal.
0.02
Cosine Power (s = 2)
Circular Normal (a = 5.55)
Wrapped Normal (σθ= 25.5o)
0.015
0.01
0.005
0
-90
-60
-30
0
30
60
90
θ (deg)
Figure C1. Comparison of the cosine-power, circular-normal and wrapped-normal
distributions with a standard deviation of 25.5 deg
C2
Appendix C Directional Wave Spreading Functions




 Previous Page
Previous Page
