H1 = H2 + ∆z
(2.135)
where
V2
H=
+y
(2.136)
2g
The term H is called the specific head, and is the height of the total head above the channel
bed.
2.6.2 Specific Energy Diagram
For simplicity, the following specific energy (often referred to as specific head) analysis is done
on a unit width of channel so that Equation 2.136 becomes:
q2
H=
+y
(2.137)
2
2gy
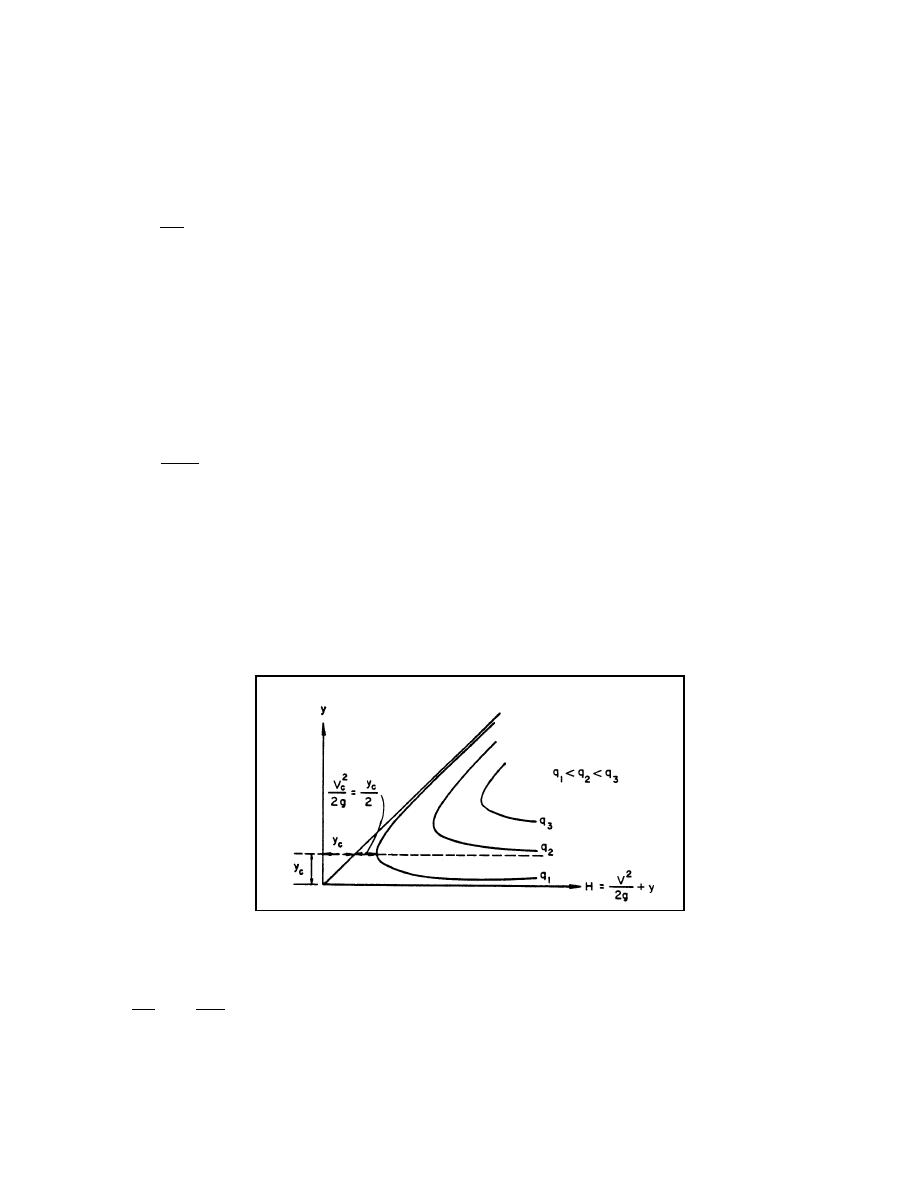
For a given q, Equation 2.137 can be solved for various values of H and y. When y is plotted as
a function of H, Figure 2.20 is obtained (Rouse 1946). There are two possible depths called
alternate depths for any H larger than a specific minimum. Thus, for specific energy larger than
the minimum, the flow may have a large depth with small velocity or small depth with large
velocity. Flow cannot occur with specific energy less than the minimum. The single depth of flow
at the minimum specific energy is called the critical depth yc and the corresponding velocity, the
critical velocity Vc = q/yc. To determine yc the derivative of H with respect to y is set equal to 0.
Figure 2.20. Specific energy diagram.
q2
dH
= 1- 3 = 0
(2.138)
dy
gy
2.39




 Previous Page
Previous Page
