2.6 STEADY RAPIDLY VARYING FLOW
2.6.1 Flow Through Transitions
Steady flow through relatively short transitions where the flow is uniform before and after the
transition can be analyzed using the Bernoulli equation. Energy loss due to friction may be
neglected, at least as a first approximation. Refinement of the analysis can be made in a second
step by including friction loss (see HEC-14, Chapter 4). For example, the water surface elevation
through a transition is determined using the Bernoulli equation and then modified by determining
the friction loss effects on velocity and depth in short reaches through the transition. Energy
losses resulting from flow separation cannot be neglected, and transitions where separation may
occur need special treatment which may include model studies. Contracting flows (converging
streamlines) are less susceptible to separation than for expanding flows. Also, any time a
transition changes velocity and depth such that the Froude number approaches unity, problems
such as waves, blockage, or choking of the flow may occur. If the approaching flow is
supercritical, a hydraulic jump may result. Unsubmerged flow through bridges or culverts can be
considered as flow through transitions.
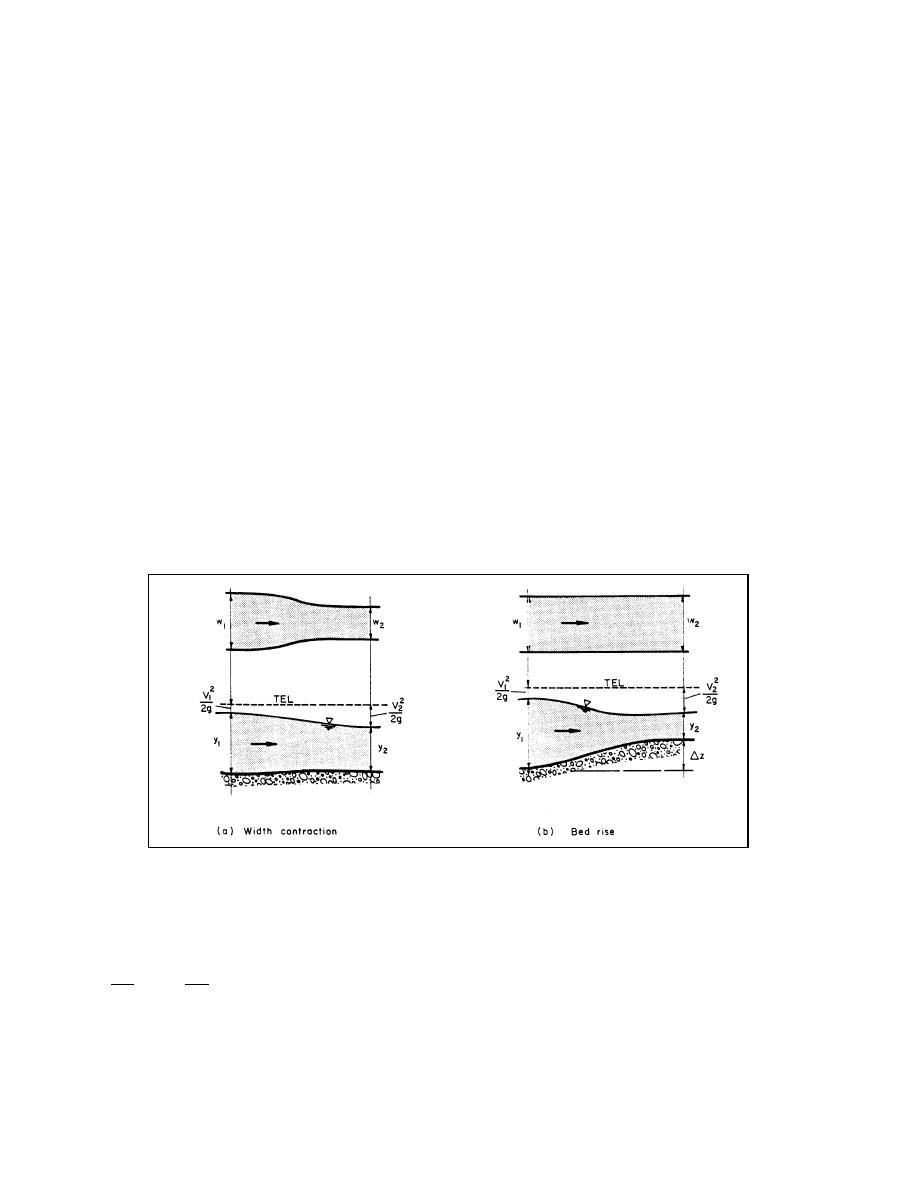
Transitions are used to contract or expand a channel width (Figure 2.19a); to increase or
decrease bottom elevation (Figure 2.19b); or to change both the width and bottom elevation. The
first step in the analysis is to use the Bernoulli equation (neglecting any head loss resulting from
friction or separation) to determine the depth and velocity changes of the flow through the
transition. Further refinement depends on importance of freeboard, whether flow is supercritical
or approaching critical conditions.
Figure 2.19. Transitions in open channel flow.
The Bernoulli equation for flow in Figure 2.19b is:
V12
V22
+ y1 =
+ y 2 + ∆z
(2.134)
2g
2g
or
2.38





 Previous Page
Previous Page
