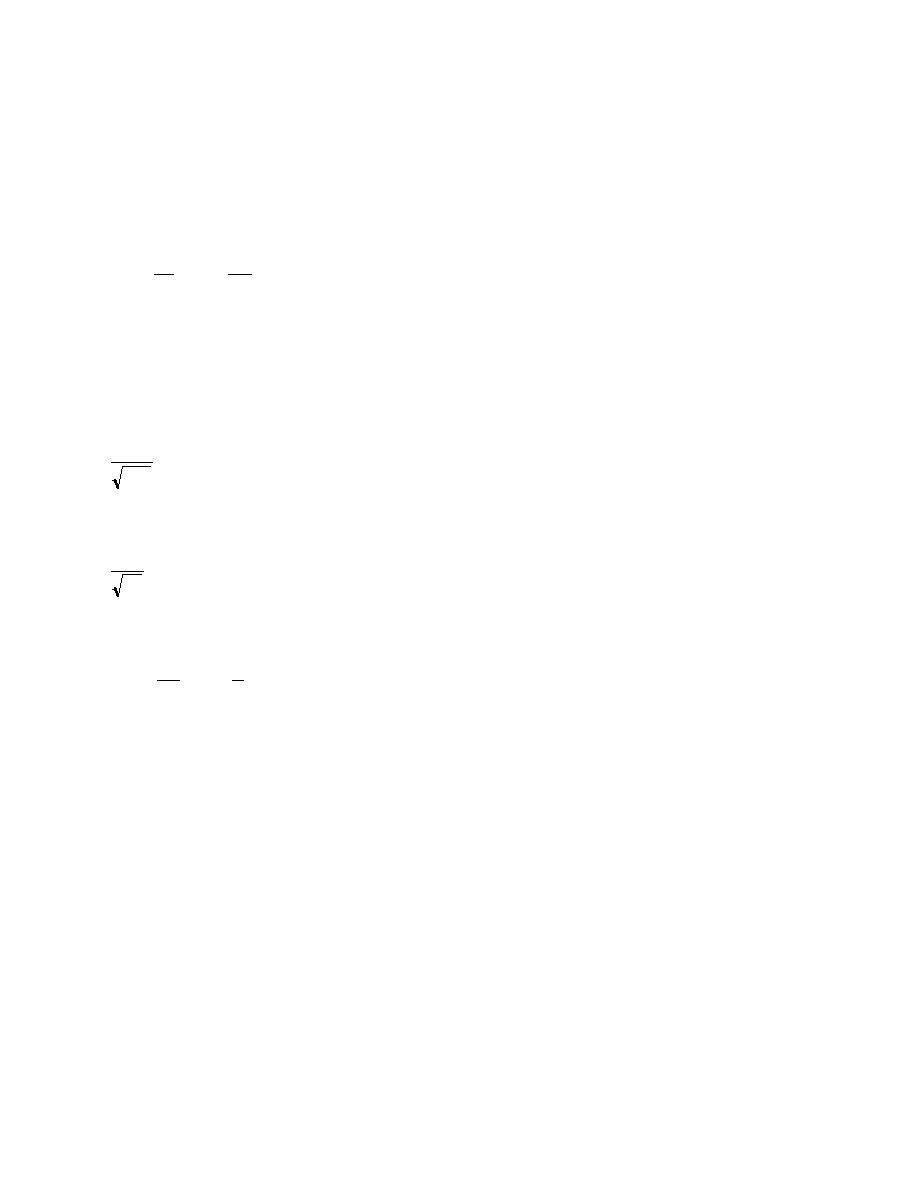
and
q = (gy 3 )
1/ 2
(2.139)
c
or
1/ 3
q2
Vc2
yc =
=2
(see Equation 2.147)
(2.140)
g
2g
Note that
Vc2 = y c g
(2.141)
or
Vc
=1
(2.142)
gy c
but
V
= Fr
(2.143)
gy
also
Vc2
3
=
+ y c = y c (see Equation 2.147)
Hmin
(2.144)
2g
2
Thus, flow at minimum specific energy has a Froude number equal to one. Flows with velocities
larger than critical (Fr > 1) are called rapid or supercritical and flow with velocities smaller than
critical (Fr < 1) are called tranquil or subcritical. These flow conditions are illustrated in Figure
2.21, where a rise in the bed causes a decrease in depth when the flow is tranquil and an
increase in depth when the flow is rapid. Furthermore, there is a maximum rise in the bed for a
given H1 where the given rate of flow is physically possible. If the rise in the bed is increased
beyond ∆zmax for Hmin then the approaching flow depth y1 would have to increase (increasing H)
or the flow would have to be decreased. Thus, for a given flow in a channel, a rise in the bed
level can occur up to a ∆zmax without causing backwater.
2.6.3 Specific Discharge Diagram
For a constant H, Equation 2.137 can be solved for y as a function of q. By plotting y as a
function of q, Figure 2.22 is obtained and for any discharge smaller than a specific maximum, two
depths of flow are possible (Rouse 1946).
2.40




 Previous Page
Previous Page
