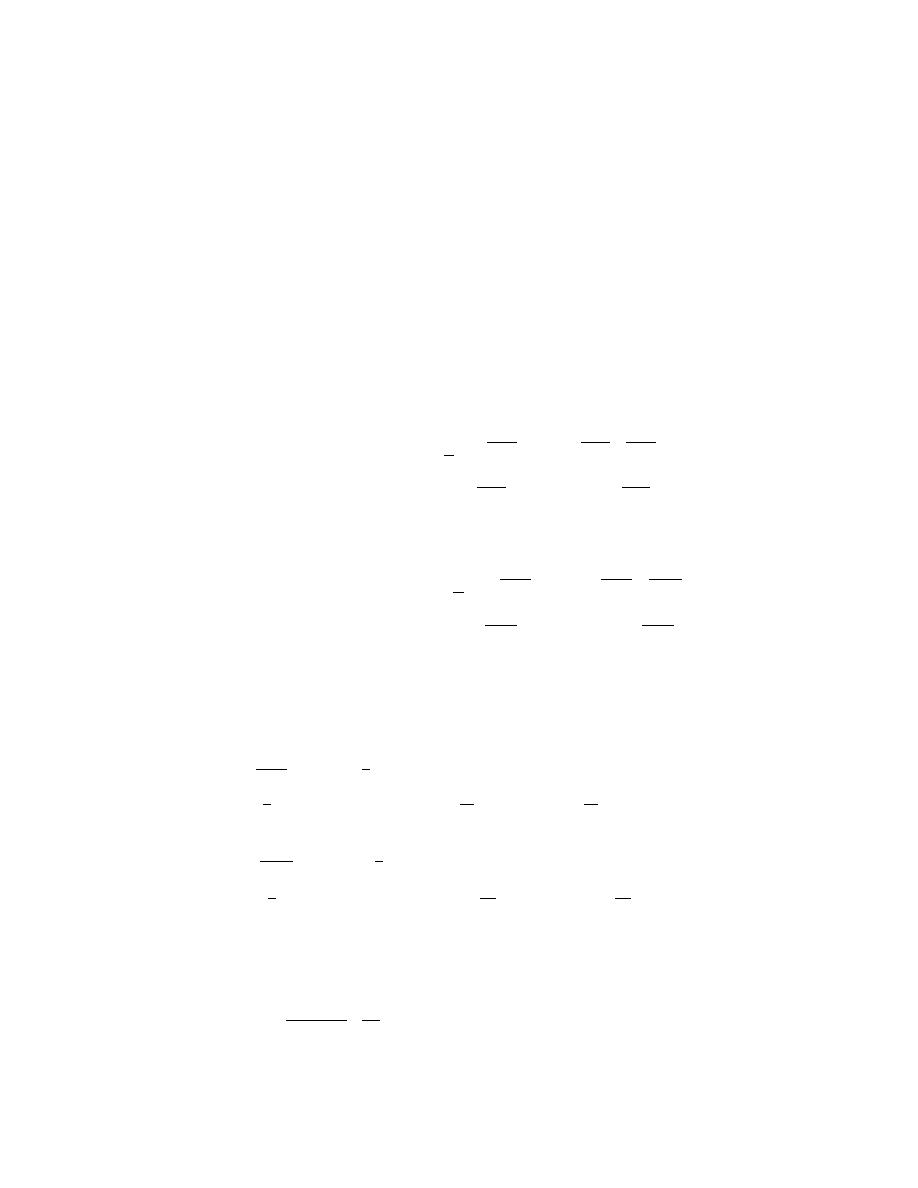
The numerical solution scheme is an implicit Crank-Nicolson scheme with a
predictor-corrector method used to provide the initial estimate. The first step in
the solution scheme is the predictor step in which values of the variables at an
intermediate time-step t = (n + )∆t are determined using known values at t =
n∆t (∆t is the time-step size). The second step is the corrector step in which pre-
dicted values at t = (n+ )∆t are used to provide an initial estimate of the values
at t = (n+1)∆t. The last step is an iterative Crank-Nicolson scheme, which is
repeated until convergence.
The partial derivatives are approximated using a forward difference scheme
for time and central difference schemes for the spatial variables. The resulting
Crank-Nicolson formulation for the weakly nonlinear form of the mass and
momentum equations (Equations 4-6) can be written as:
δt η = - δ(1)un+1/ 2 -δ(y1)vn+1/ 2
(21)
x
f
f
)
)
(
(
n+1/ 2 x 2 (1) n+1/ 2 x n+1/ 2 y
1
(
)
n+1/ 2
δt uα + f4δ u + f2δxxuα = - gδ η
- δ uα
- δy vα
(2)
(1)
(1)
uα
α
x
x
x
2
)
()
(
δ(1) (h) δ δ(1) vn+1/ 2 y + δ(1) (h) δ δ(1) vn+1/ 2 x
(22)
- f4 y
α
α
tx
x
ty
- f2δt δxyvα+1/ 2
n
)
)
(
(
n+1/ 2 y 2 (1) n+1/ 2 x n+1/ 2 y
1
(
)
n+1/ 2
δt vα + f4δ v + f2δ yy vα = - gδ η
- δ vα
- δx vα
(2)
(1)
(1)
uα
α
y
y
y
2
)
) (23)
(
(
- f4 δ(y1) (h) δt δ(x1) uα+1/ 2
y
x
+ δ(x1) (h) δt δ(y1) uα+1/ 2
n
n
- f2δt δ xyuα+
n 1/ 2
where the volume flux densities uf and vf are given by:
u f i+1/ 2, j = h + η uα i+1/ 2, j + h f1 (δxxuα + δxyvα )
x
x
(24)
()
()
+ h f3 2δ(x1) (h)δ(x2)uα + δ(x1) (h)δ(y1) vα + δ(y1) (h) δ(x1) vα
x
x
y
v f i, j+1/ 2 = h + η vα i, j+1/ 2 + h f1 (δxyuα + δ yyvα )
y
y
(25)
( )+δ
(u )
+ h f3 2δ(y1) (h)δ(y2)vα + δ(x1) (h)δ(y1) uα
y
x
y
(h) δ
(1)
(1)
α
y
x
The parameters f1 to f4 are given by:
( zα + h)2 h2
f1 =
-
(26a)
2
6
13
Chapter 3 Numerical Solution




 Previous Page
Previous Page
