computational time, the existing first order scheme (without smoothing) was found to be the most efficient by a
significant margin. The Lax-Wendroff scheme, in combination with the smoothing, took approximately 3.5 times
longer than the first order approach. The QUICKEST/ULTIMATE scheme required twice the computer time of the
Lax-Wendroff scheme.
The first order downwind scheme was highly efficient but did not perform as well as other approaches due to the
excessive numerical diffusion of this scheme. Interestingly, the relative merits of this scheme were improved when
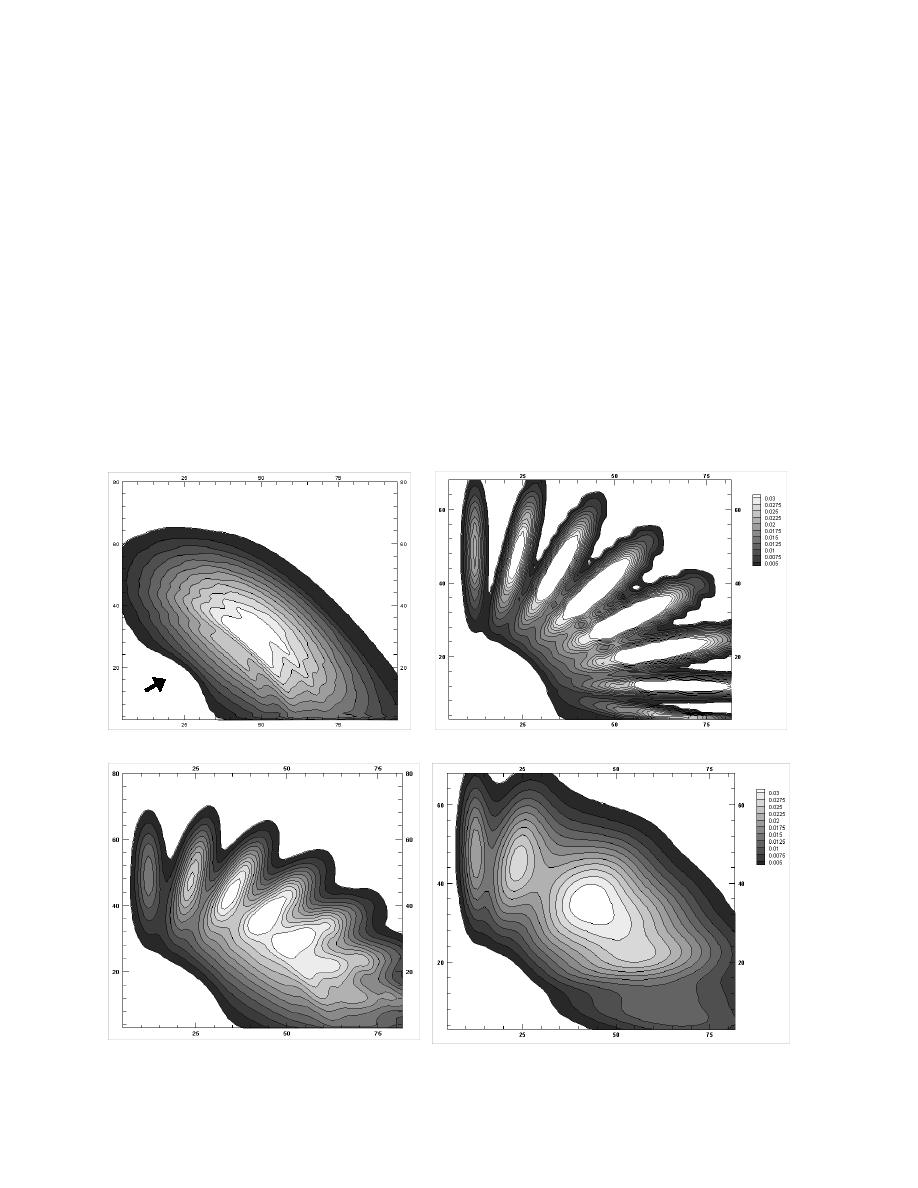
great circle effects were considered in the computations. Figure 6d shows an example solution for the first order
scheme when curvature is included.
The general conclusions from our experimentation were:
A second order scheme in combination with a diffusion operator is likely sufficient for improving the
overall accuracy of swell propagation without placing an excessive computational burden on a 2nd
generation wave model.
Concepts and approaches to the development of an efficient GSE diffusion operator need to be improved.
Ultimately, the first order downwind scheme was selected for initial application to the Pacific Ocean and the results
presented in this paper are based on these results; however, efforts are continuing to improve the propagation
numerics in WAVAD.
(b) QUICKEST/ULTIMATE 15 degree
(a) QUICKEST/ULTIMATE 1 degree
directional resolution
directional resolution
(c) Lax-Wendroff with Tolman Bin Smoothing
(d) First Order with Great Circle Effects
Figure 6. Contours of Energy from Experimentation with Wave Model Propagation Schemes
[After 7 days of simulation; Grid dimensions in degrees; Contour interval=25 cm2]




 Previous Page
Previous Page
