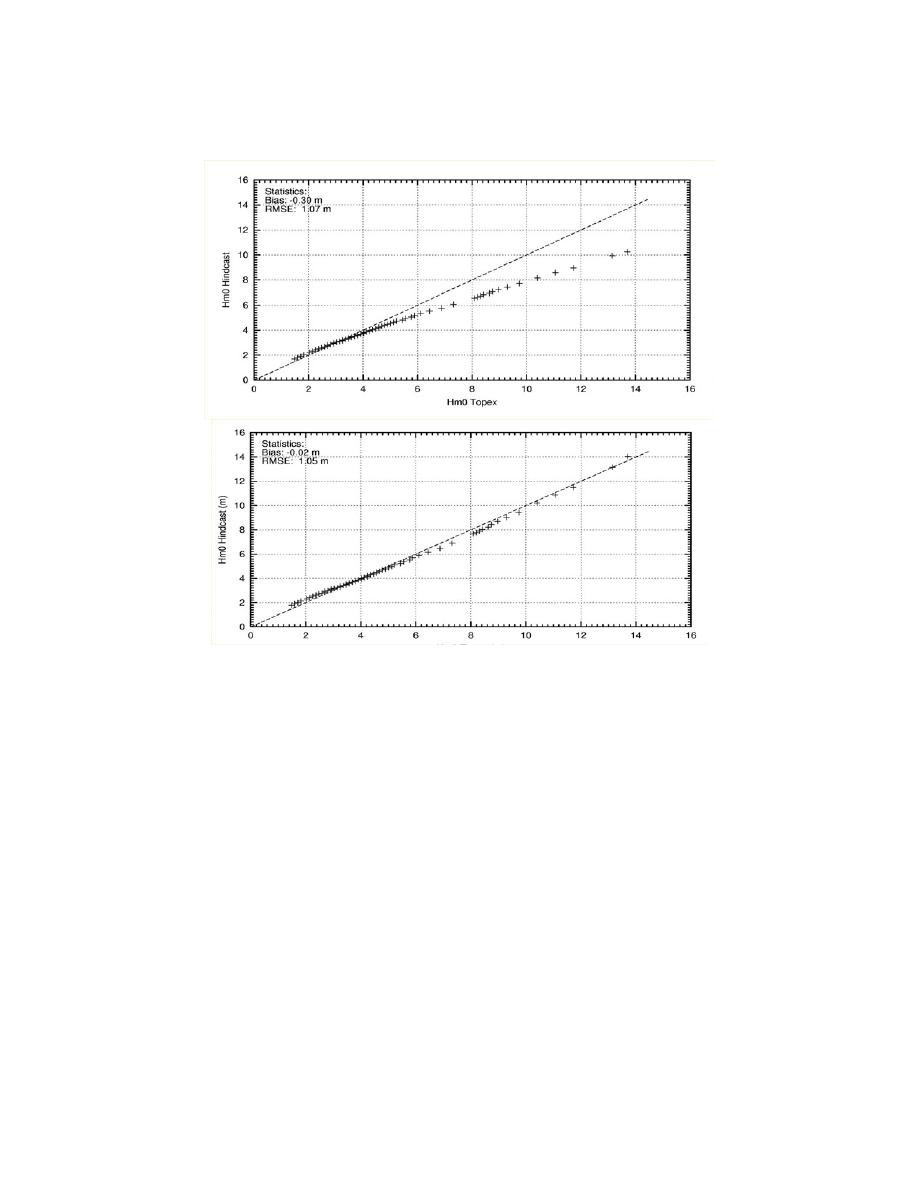
comparisons over the range from 1% to 99.95%. Figure 5 shows q-q plots for the southern mid-latitudes before and
after the wind speed factoring was applied.
Figure 5. Effect of Wind Speed Factoring on Quantile-Quantile Lower Mid-Latitudes.
Top plot is unfactored winds while the bottom plot includes factored winds.
The wind speed factoring ultimately applied to the model had the following form:
Umodel = UNCEP * (1 + (UNCEP-14.5)*0.026)
Northern Region:
Southern Region:
Umodel = UNCEP * (1 + (UNCEP-13.5)*0.027)
Where Umodel is the wind speed input to the wave model and UNCEP is the 10 m interpolated NCEP wind speed.
5.2 Swell Propagation and Computational Requirements
The appropriate simulation of the propagation of ocean swell waves has proven problematic in wave models due to
practical limitations in model resolution in both physical and spectral space. In the latter case, as the energy
spectrum in a numerical wave model is divided into a discrete number of frequency and directional bands,
continuous fields of swell waves fragment into discrete parcels of energy as they propagate in space. This
fragmentation is known as the Garden Sprinkler Effect (GSE).
A series of numerical experiments were conducted to assess various methodologies for alleviating the GSE. This
phenomenon has been explored by others (for example, Booij and Holthuijsen (1987); Tolman (2001)); however,
in our case there was a strong emphasis on computational speed. The original WAVAD model, which utilizes a
standard first order upwind propagation scheme, is a highly efficient model. For the Pacific Ocean (160x132 grid), a
ten-year simulation required only 50 hours of computational time on a Pentium4 1.4 GHz personal computer.
However, the first order scheme was found to be excessively diffusive and did not appropriately rid the model of




 Previous Page
Previous Page
