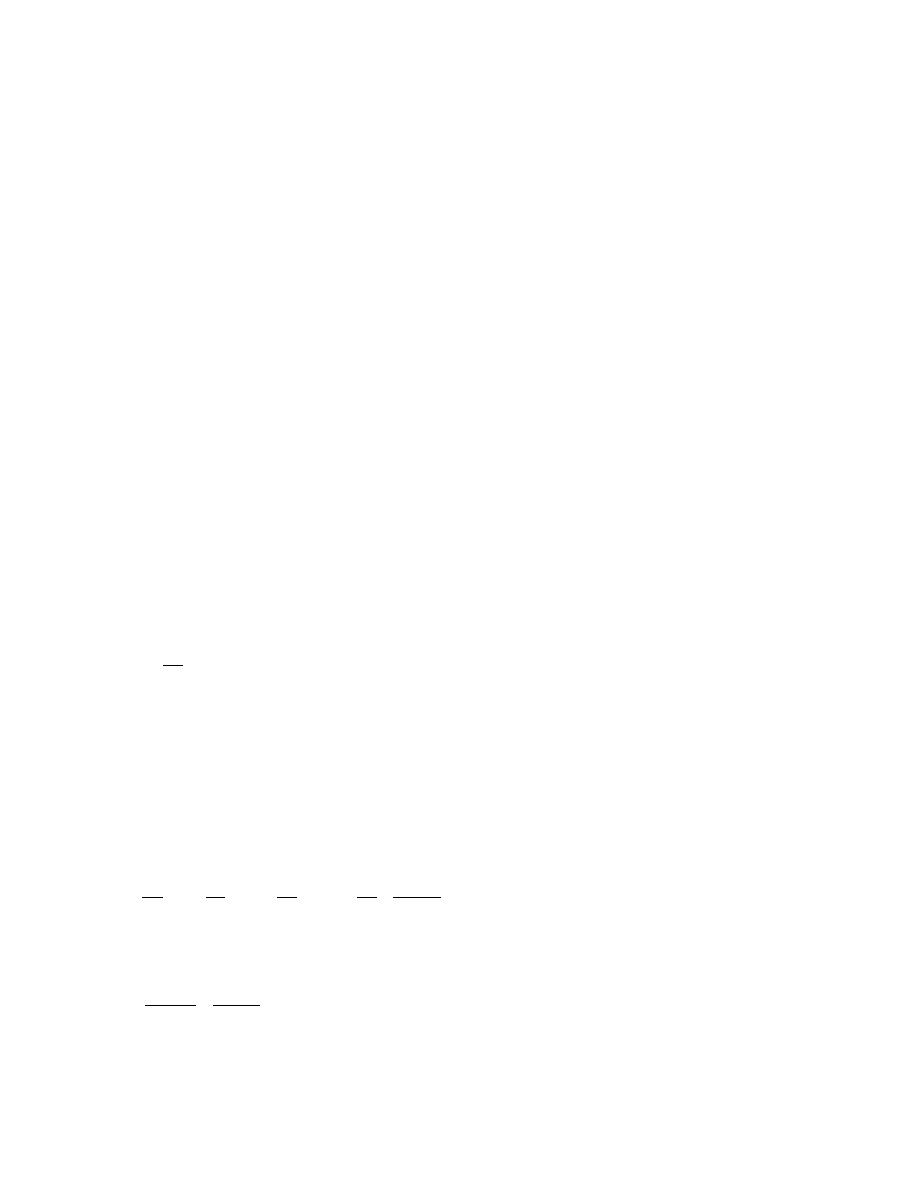
Along the interior boundaries of the streamtube there is a shear stress resulting from the
condition that the fluid velocity inside the streamtube may not be the same as the velocity of the
fluid surrounding the streamtube. The rate at which the fluid in the streamtube does shear work
on the control volume is:
W τ = τP dx v
(2.34)
where τ is the average shear stress on the streamtube boundary, P is the average perimeter of
the streamtube, dx is the length of the streamtube and v is the fluid velocity at the streamtube
boundary. The product P dx is the surface of the streamtube subjected to shear stresses.
Then for steady flow in the streamtube, the statement of the conservation of energy in the
streamtube shown in Figure 2.3 is:
ρ 2 e 2 v 2 dA 2 - ρ1 e1 v 1 dA 1 = p1 v 1 dA 1 - p 2 v 2 dA 2 - τPv dx
(2.35)
The conservation of mass for steady flow in the streamtube is (according to Equation 2.16)
v 2 dA 2 = v 1 dA 1 = dQ
(2.36)
Now Equation 2.35 reduces to
(ρ1 e1 + p1 ) dQ - (ρ 2 e 2 + p 2 ) dQ = τPv dx
(2.37)
The energy per unit mass e is the sum of the internal, kinetic and potential energies or
v2
e =u+
+ gz
(2.38)
2
where:
u
=
Internal energy associated with the fluid temperature
v
=
Velocity of the mass fluid
g
=
Acceleration due to gravity
z
=
Elevation above some arbitrary reference level
This expression for e is substituted in Equation 2.37 to yield
2
v2
τPvdx
v1
p1
p
u1 +
+ gz1
= u 2 + 2 + gz 2 + 2 +
(2.39)
ρ
ρ
ρdQ
2
2
By dividing through by g and defining the head loss hl as follows:
u 2 - u1 τPvdx
hl =
+
(2.40)
ρgdQ
g
2.10




 Previous Page
Previous Page
