2.2.2 Conservation of Linear Momentum
The curved reach of the river shown in Figure 2.1 is rather complex to analyze in terms of
Newton's Second Law because of the curvature in the flow. Therefore, as a starting point, the
differential length of reach dx is isolated as a control volume.
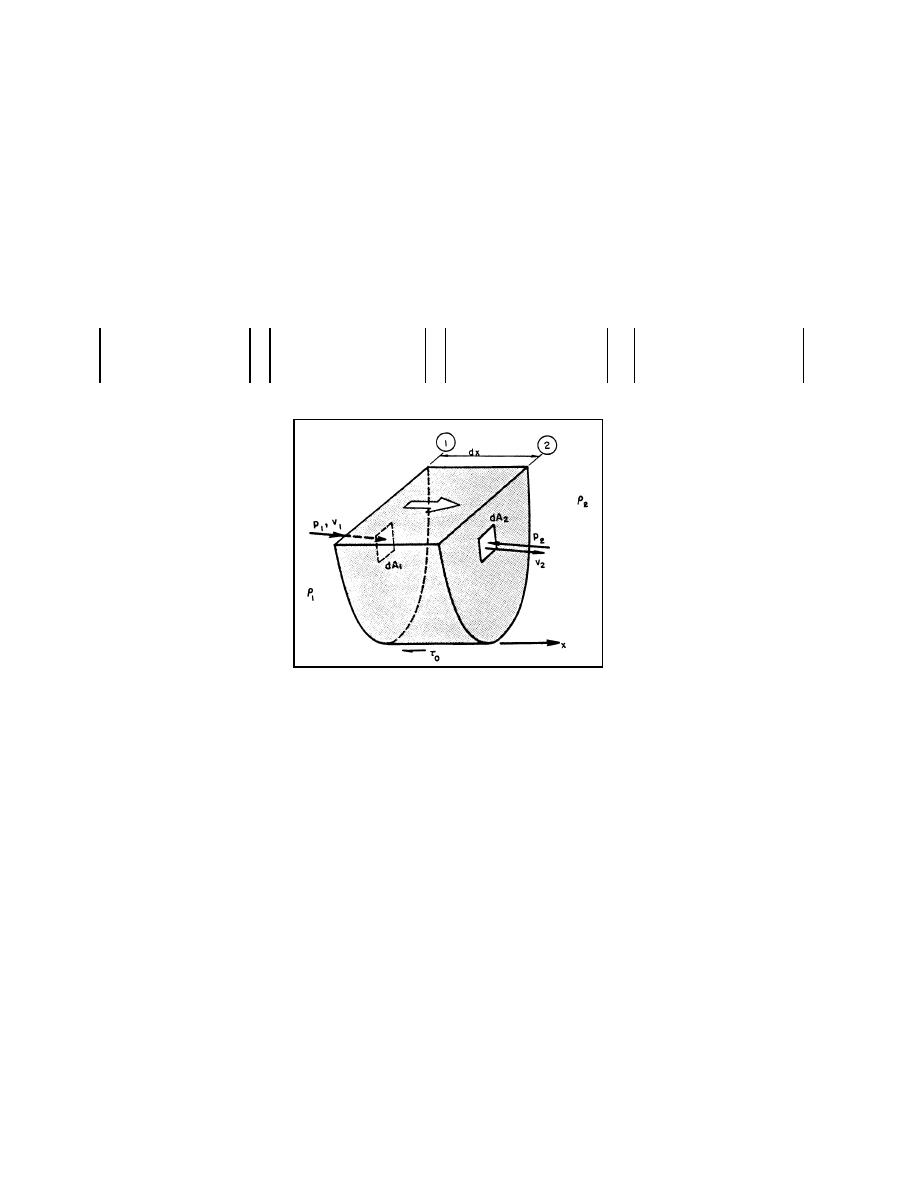
For this control volume, shown in Figure 2.2, the pressure terms p1 and p2 are directed toward
the control volume in a direction normal to the Sections 1 and 2. The shear stress τo is exerted
along the interface between the water and the wetted perimeter and is acting in a direction
opposite to the axis x. The statement of conservation of linear momentum is:
Sum of the forces
Time rate of change
Flux of momentum
Flux of Momentum
acting on the fluid
=
+ of momentum in
- into the control
out of the control
in the control volume
the control volume
volume
volume
Figure 2.2. The control volume for conservation of linear momentum.
The terms in the statement are vectors so we must be concerned with direction as well as
Consider the conservation of momentum in the direction of flow (the x-direction in Figure 2.2). At
the outflow section (section 2), the flux of momentum out of the control volume through the
differential area dA2 is:
ρ2v2 dA2 v2
(2.17)
Here ρ2 v2 dA2 is the mass flux (mass per unit of time) and ρ2 v2 dA2 v2 is the momentum flux
through the area dA2.
Flux of momentum
A ρ 2 v 2 dA 2 v 2
(2.18)
out of the control
=
2
volume
Similarly, at the inflow section (section 1),
2.6




 Previous Page
Previous Page
