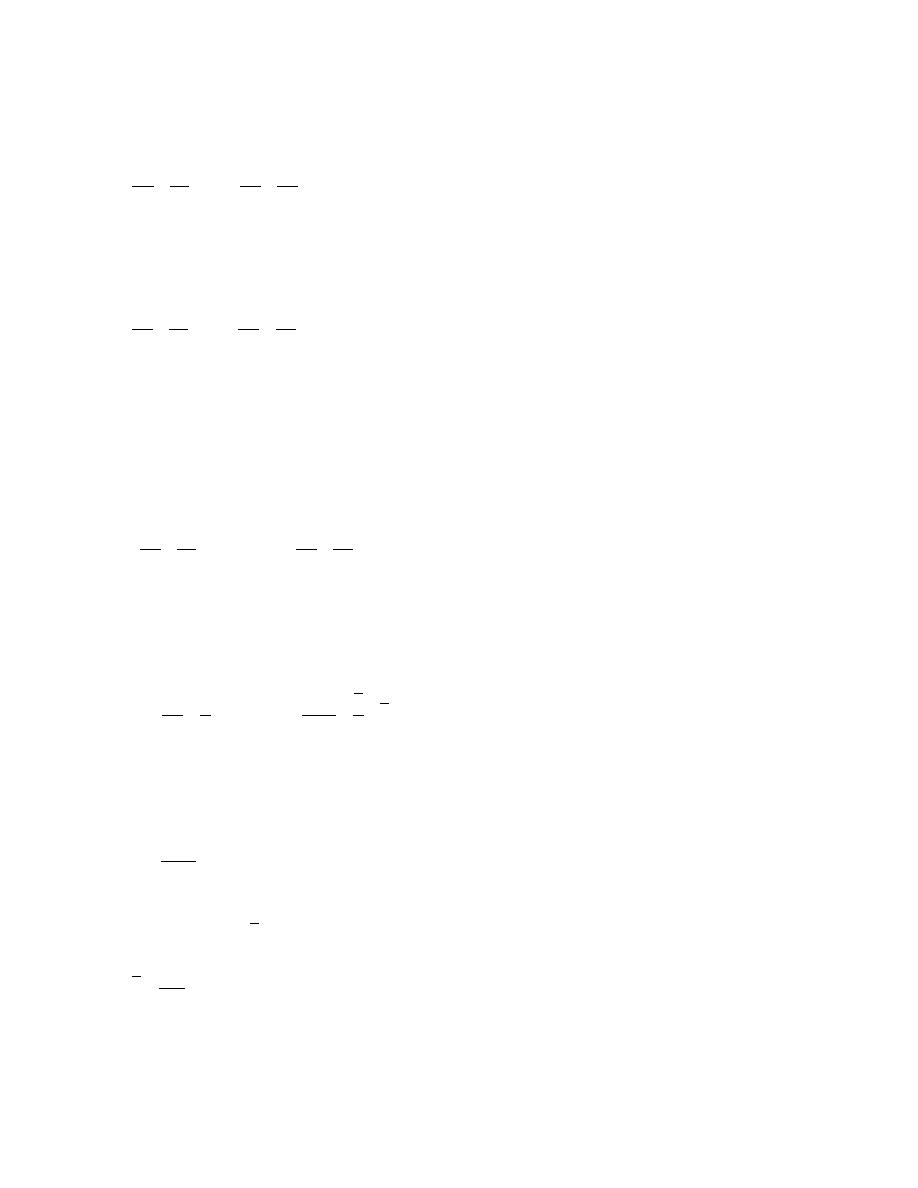
The energy equation for the streamtube becomes
2
v 2 p2
v 1 p1
+ z1 = 2 +
+
+ z 2 + hl
(2.41)
2g γ
γ
2g
If there is no shear stress on the streamtube boundary and if there is no change in internal
energy (u1 = u2), the energy equation reduces to:
2
v 2 p2
v 1 p1
+
+ z1 = 2 +
+ z 2 = cons tan t
(2.42)
2g γ
2g γ
which is the Bernoulli Equation.
Generally, there is not sufficient information available to do a differential streamtube analysis of a
reach of river, so appropriate changes must be made in the energy equation. A reach of river
such as that shown in Figure 2.1 can be pictured as a bundle of streamtubes. We know the
statement of the conservation of energy for a streamtube. It is Equation 2.41 which can be
written:
v 1 p1
v 2 p2
2
+ z1 v dA = 2 +
+ z 2 v dA + hl vdA
+
(2.43)
2g γ
2g γ
because v1 dA1 = v2 dA2 = vdA for the streamtube.
The common form of the energy equation used in open channel flow is derived by integrating
Equation 2.43 over the cross-section area:
αV 2 p
v2 p
+ + z vdA =
+ + z Q
(2.44)
A 2g γ
γ
2g
where:
=
Kinetic energy correction factor defined by the expression
α
1
α=
v 3 dA
(2.45)
A
V3A
to allow the use of average velocity V rather than point velocity v. The average pressure over the
cross-section is p , defined as:
1
p=
p vdA
(2.46)
A
VA
2.11





 Previous Page
Previous Page
