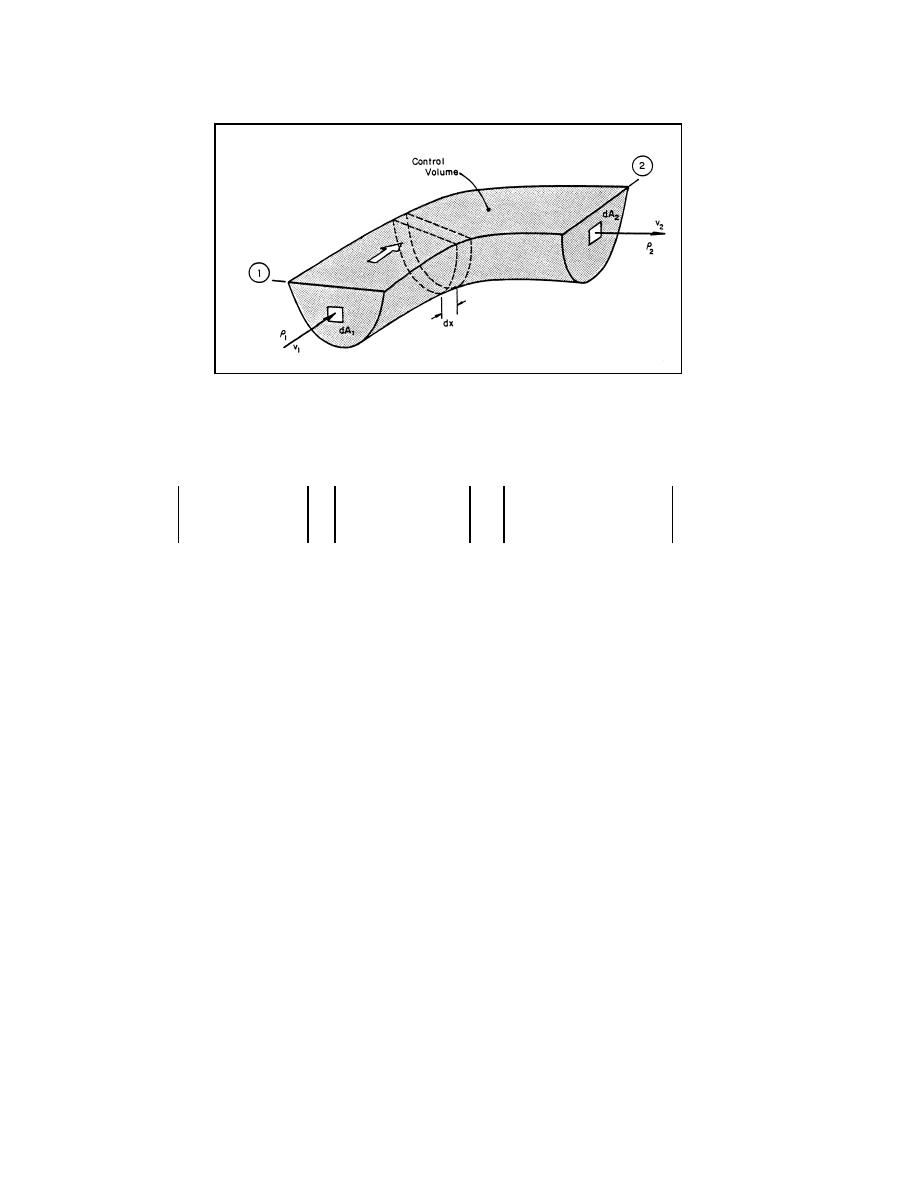
Figure 2.1. A river reach as a control volume.
The statement of the conservation of mass for this control volume is
Mass flux
Mass flux
Time rate of change
out of the
-
into the
+
in mass in the
=0
control volume
control volume
control volume
Mass can enter or leave the control volume through any or all of the control volume surfaces.
Rainfall would contribute mass through the surface of the control volume and seepage passes
through the interface between the water and the banks and bed. In the absence of rainfall,
evaporation, seepage and other lateral mass fluxes, mass enters the control volume at section 1
and leaves at section 2.
At section 2, the mass flux out of the control volume through the differential area dA2 is ρ2 v2 dA2.
The values of ρ2 and v2 can vary from position to position across the width and throughout the
depth of flow at section 2. The total mass flux out of the control volume at section 2 is the
integral of all ρ2 v2 dA2 through the differential areas that make up the cross-section area A2, and
may be written as:
Mass flux
A ρ 2 v 2 dA 2
out of the
=
(2.9)
2
control volume
Similarly
Mass flux
A ρ1 v 1 dA 1
into the
=
(2.10)
1
control volume
The amount of mass inside a differential volume dV inside the control volume is ρ dV and
2.4




 Previous Page
Previous Page
