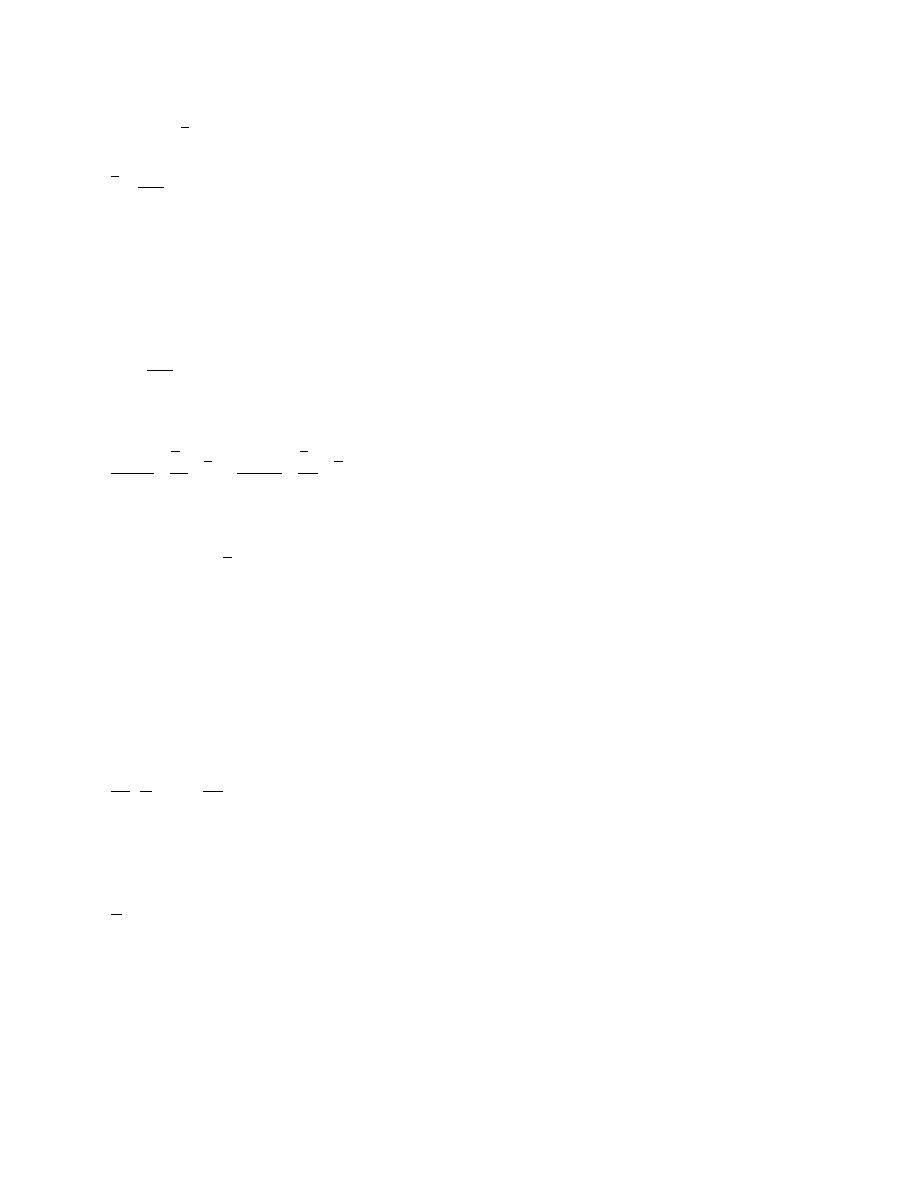
The term z is the average elevation of the cross-section defined by the expression:
1
z=
zvdA
(2.47)
A
VA
and Q is the volume flow rate or the discharge. By definition
Q=
vdA
(2.48)
A
Also
1
HL =
A hl vda
(2.49)
VA
In summary, the expression for conservation of energy for steady flow in a reach of river is written
α1 V12 p1
α 2 V22 p 2
+
+ z1 =
+
+ z 2 + HL
(2.50)
γ
γ
2g
2g
The tendency in river work is to neglect the energy correction factor even though its value may
be as large as 1.5. Usually it is assumed that the pressure is hydrostatic and the average
elevation head z is at the centroid of the cross-sectional area. However, it should be kept in
mind that Equations 2.45, 2.46, and 2.47 are the correct definitions of the terms in the energy
equation. An example problem illustrating the calculation of α and β for a stream is provided in
Section 2.14 (SI) and 2.15 (English).
2.3 HYDROSTATICS
When the only forces acting on the fluid are pressure and fluid weight, the differential equation of
motion in an arbitrary direction x is
∂ p
a
+ z = x
(2.51)
∂x γ
g
In steady uniform flow (and for zero flow), the acceleration is zero and we obtain the equation of
hydrostatics
p
+ z = Cons tan t
(2.52)
γ
However, when there is acceleration, the piezometric head varies in the flow field. That is, the
piezometric head is not constant in the flow. This is illustrated in Figure 2.4. In Figure 2.4a the
pressure at the bed is hydrostatic and equal to γyo whereas in the curvilinear flow (Figure 2.4b)
the pressure is larger than γyo because of the acceleration resulting from a change in direction.
2.12





 Previous Page
Previous Page
