Variables of interest for steady uniform flow are: (1) the mean velocity V, (2) the discharge Q,
(3) the velocity distribution v(y) in the vertical, (4) the head loss HL through the reach, and (5) the
shear stress, both local τ and at the bed τo. These variables are interrelated.
2.4.2 Shear Stress, Velocity Distribution, and Average Velocity
Shear stress τ is the internal fluid stress which resists deformation. The shear stress exists only
when fluids are in motion. It is a tangential stress in contrast to pressure, which is a normal
stress.
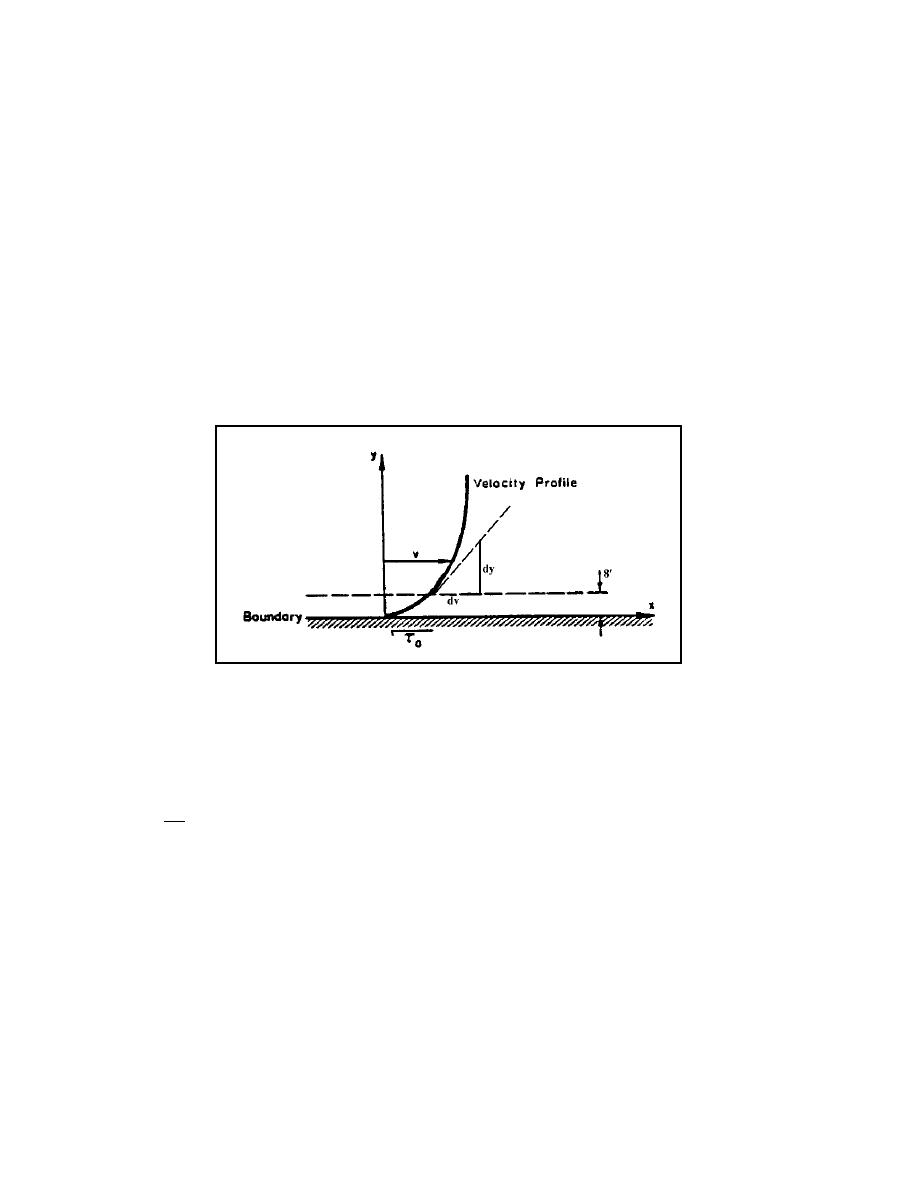
The local shear stress at the interface between the boundary and the fluid can be determined
quite easily if the boundary is hydraulically smooth; that is, if the roughness at the boundary is
submerged in a viscous sublayer as shown in Figure 2.7.
Figure 2.7. Hydraulically smooth boundary.
Here, the thickness of the laminar sublayer is denoted δ′. In laminar flow, the shear stress at the
boundary is:
dv
τ o = at y = 0
(2.66)
dy
The velocity gradient is evaluated at the boundary. The dynamic viscosity is the proportionality
constant relating boundary shear and velocity gradient in the viscous sublayer.
When the boundary is hydraulically rough, the thickness of the laminar sublayer is very small
compared to the roughness height. The paths of fluid particles in the vicinity of the boundary are
shown in Figure 2.8.
The velocity at a point near the boundary fluctuates randomly about a mean value. The random
fluctuation in velocity characterizes turbulent flows. As shown in Figure 2.9a, the particle has a
vertical component of velocity vy as well as a horizontal component vx.
2.16





 Previous Page
Previous Page
