cos θ tan φ
cos 18.4 tan 35
S.F. =
=
= 1.59
n′ tan φ + sin θ cos β 0.154 tan 35 + sin 18.4 cos 11
Thus, with a stability factor of 1.59, this rock is more than adequate to withstand the flow
velocity.
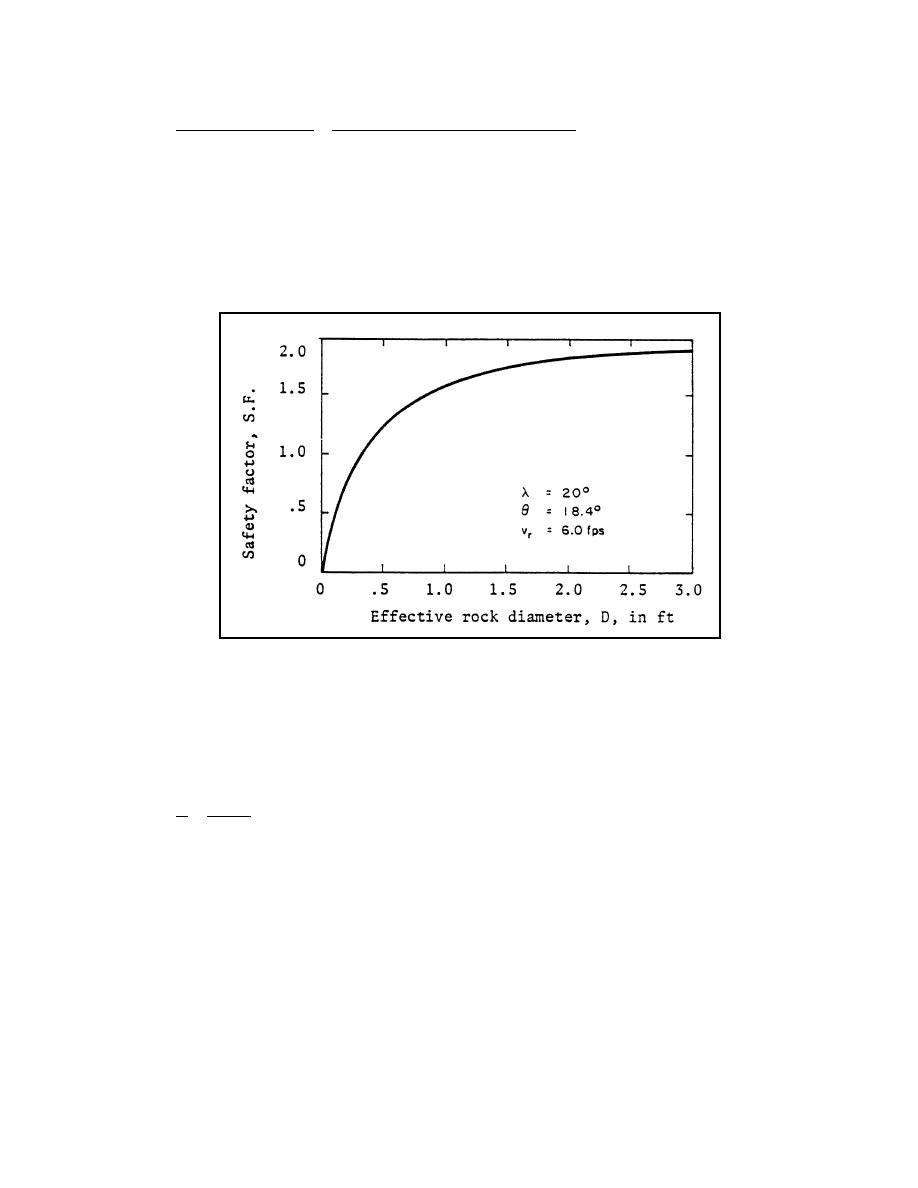
By repeating the above calculations over the range of interest for Dm (with φ = 35), the curve
given in Figure 6.37 is obtained. This curve shows that the incipient motion rock size is
approximately 0.107 m and the maximum stability factor is less than 2.0 on the 3:1 side slope.
Figure 6.37. Stability factors for various rock sizes on a side slope.
The stability factor of a particular side slope riprap design can be increased by decreasing the
side slope angle θ. If the side slope angle is decreased to zero degrees, then Equation 6.3 is
applicable and
1
1
S.F. =
=
= 4.93
η 0.203
The curve in Figure 6.38 relates the stability factor and side slope angle of the embankment
(for λ = 20, Dm = 1.0 ft and Vr = 6.0 fps). The curve is obtained by employing Equations 6.3,
6.4, 6.16, and 6.6 for various values of θ.
6.12.4 PROBLEM 4 Riprap Design on an Abutment
o
(a) Consider a spill through abutment with side slope θ = 18.5 (3:1 side slope). The flow
o
fps and angle with the horizontal λ = 20 . The specific gravity of the available rock is 2.65.
Determine the size of riprap in this area required to resist the erosive force of water.
6.68




 Previous Page
Previous Page
