coarser particles, settling is rapid and particles that are in suspension tend to concentrate
nearer the bed.
The suspended bed sediment discharge in Newtons or lbs per second per unit width of
channel, qs, for steady, uniform two-dimensional flow is
y
qS = γ s ao vcdy
(4.2)
where v and c vary with y and are the time-averaged flow velocity and volumetric
concentrations, respectively, and γs is the weight per unit volume of the suspended sediment.
The integration is taken over the depth between the distance "a" above the bed and the
bed layer. Sediment movement below this level is considered bed load rather than suspended
load.
The discharge of suspended sediment for the entire stream cross-section, QS, is obtained by
integrating Equation 4.2 over the cross section to give
QS = γ SQC
(4.3)
where:
=
Average suspended-sediment concentration by volume
C
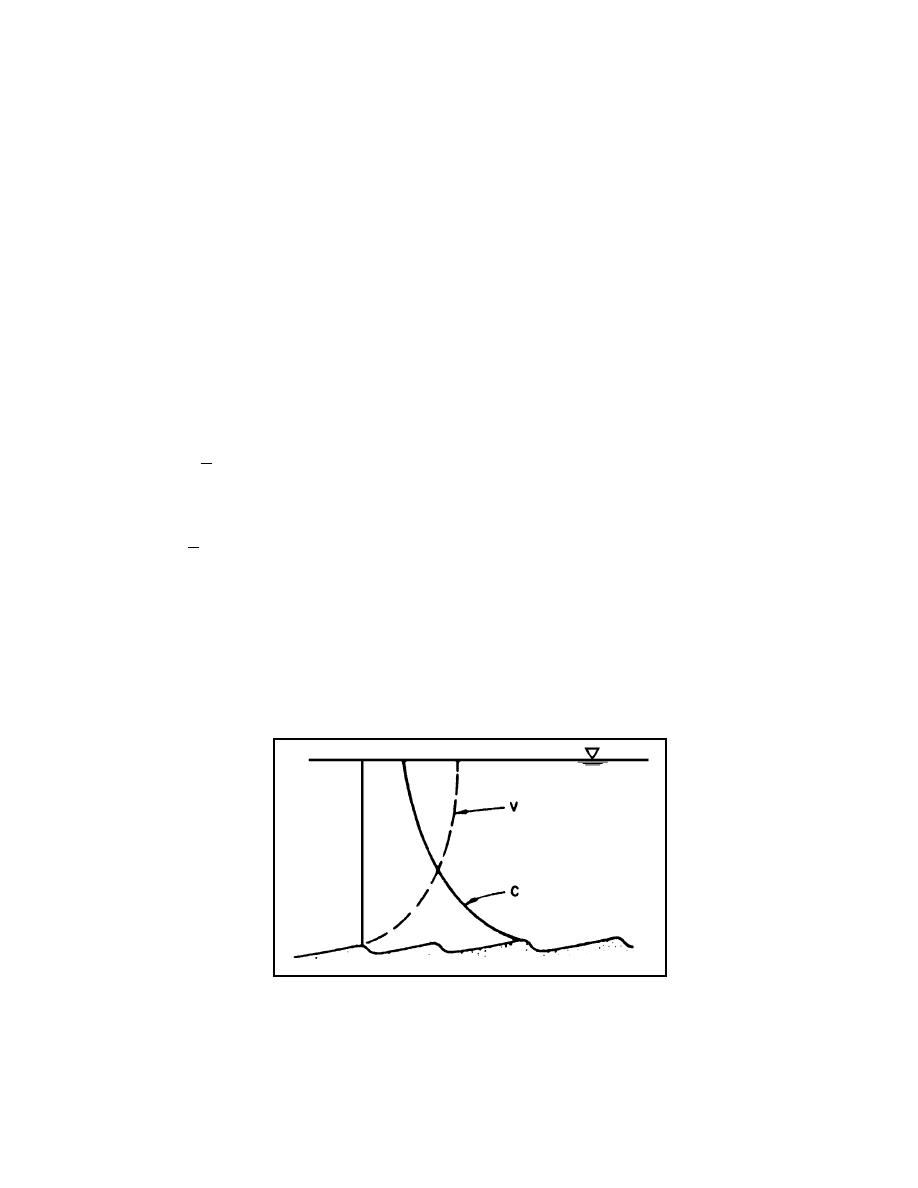
The vertical distribution of both the velocity and the concentration vary with the mean velocity
of the flow, bed roughness and size of bed material. The distributions are illustrated in
Figure 4.3. Also v and c are interrelated. That is, the velocity and turbulence at a point is
affected by the sediment at the point, and the sediment concentration at the point is affected
by the point velocity. Normally this interrelation is neglected for low sediment concentrations
or a coefficient applied to compensate for it.
Figure 4.3. Schematic sediment and velocity profiles.
To integrate Equation 4.2, v and c must be expressed as functions of y. The one-dimensional
gradient type diffusion equation is employed to obtain the vertical distribution for c and the
logarithm velocity distribution is assumed for v in turbulent flows.
4.7





 Previous Page
Previous Page
