Z
Xy
a
yo - y
yo
dy
2.5 ln 30.2
qS = γV* c a
(4.13)
k S
a
yo - a
y
Many investigators have solved this equation through integration. The assumptions and
integration made by Einstein are presented in Section 4.5.2. An example calculation for a
suspended sediment concentration profile is given in Section 4.12 (SI) and 4.13 (English).
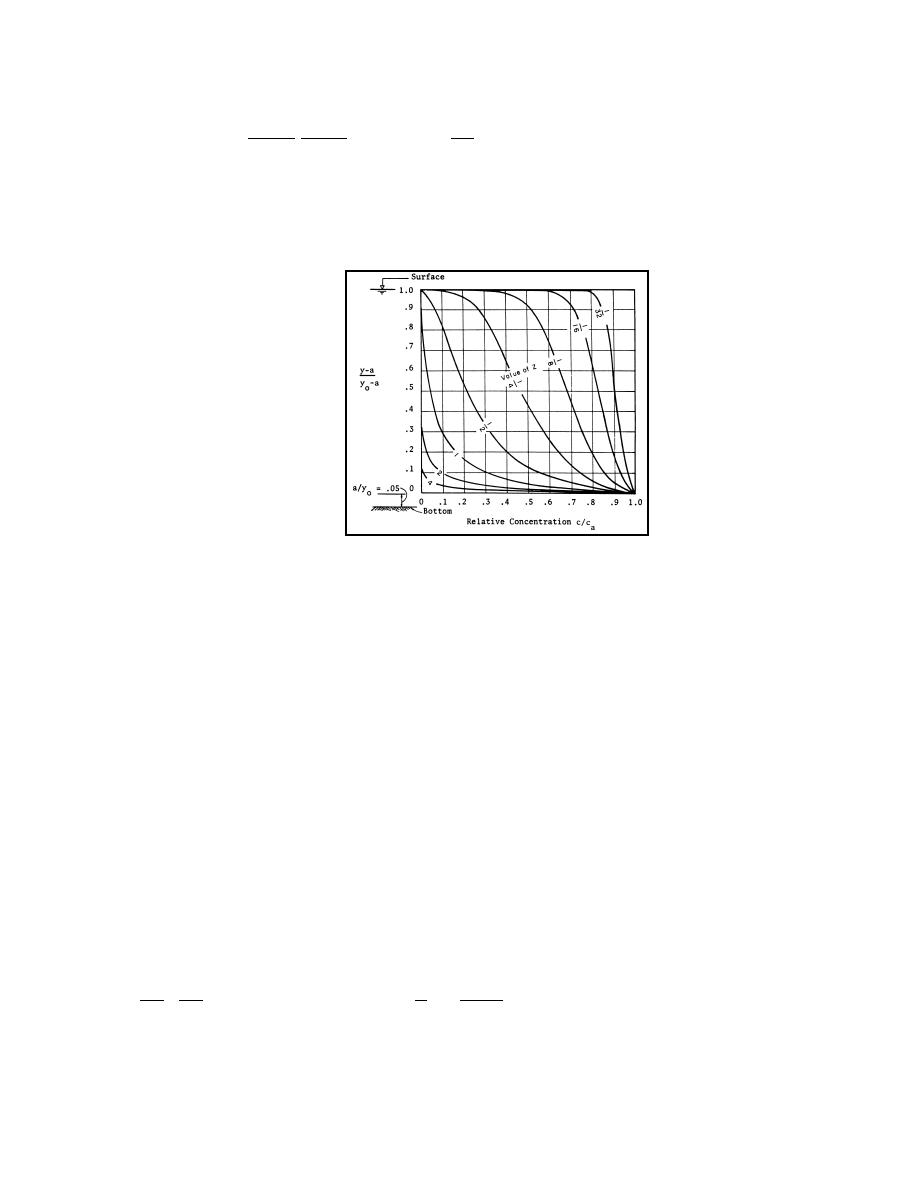
Figure 4.4. Graph of suspended sediment distribution (Rouse 1937).
4.5 BED SEDIMENT DISCHARGE
In this section, three classic sediment transport formulae are discussed in detail to illustrate
sediment transport processes. These are the Meyer-Peter and Mller (1948), Einstein (1950),
and Colby (1964) methodologies. The Meyer-Peter and Mller bedload equation (Section
4.5.1) is applicable to streams with bed material consisting of sand, gravel, and cobbles. The
Einstein (Section 4.5.2) and Colby (Section 4.5.4) methods are bed material load equations
used for sand-bed streams. In Section 4.7, power function sediment transport relationships are
discussed to provide a practical method for quick sediment transport calculations. The Yang
sand and gravel total load equations are also included (Section 4.8) because of their frequent
application and wide acceptance.
4.5.1 Meyer-Peter and Mller Bed Load Equation
Meyer-Peter and Mller (1948) developed the following bed load equation based on
experiments with sand particles of uniform sizes, sand particles of mixed sizes and density,
natural gravel, lignite, and barite:
2/3
3/2
1/ 3
γs - γ
K B
γ
Qb
γy o S f = B′(γ s - γ )Dm + B
2/3
γ
(4.14)
qB
Q
K
g
r
s
4.10





 Previous Page
Previous Page
