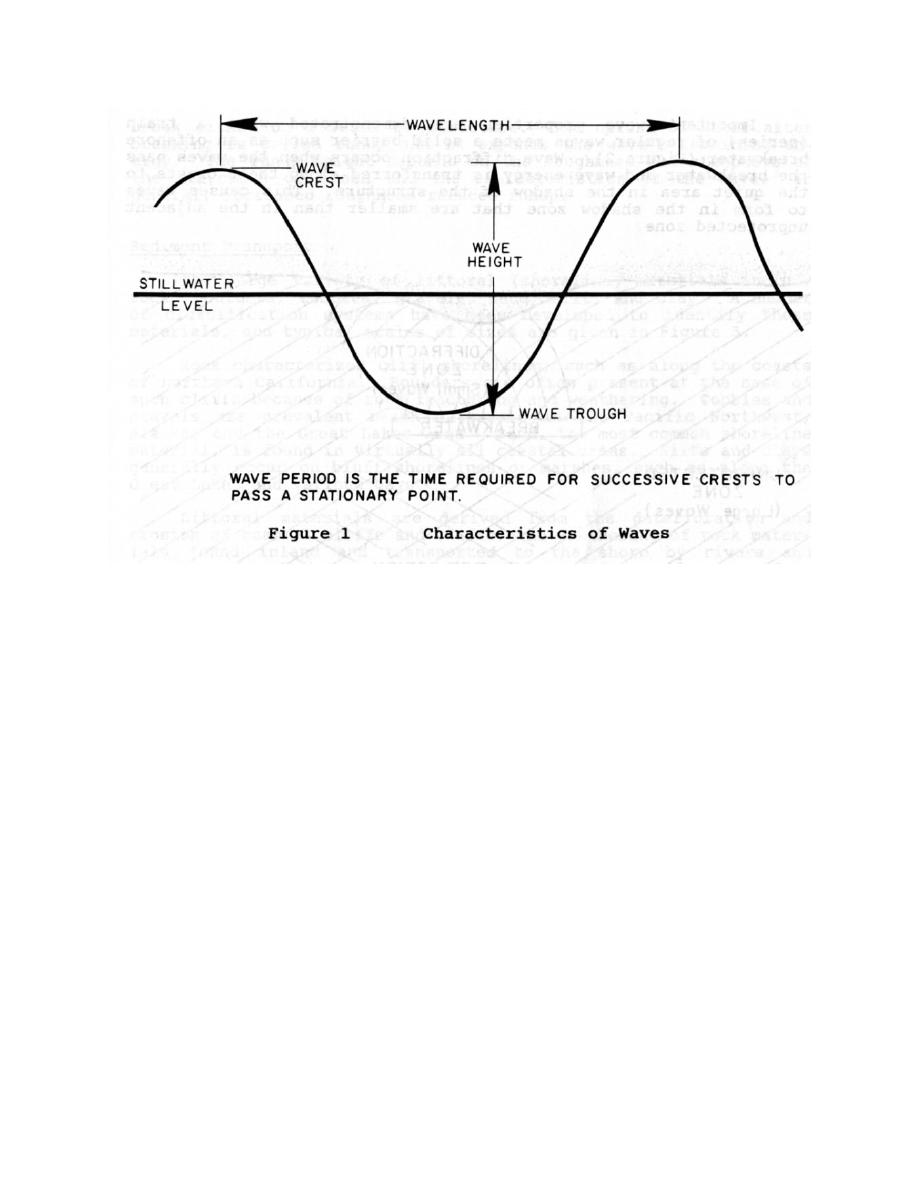
As a wave moves through deep water (depths greater than one-half the wavelength), the celerity
and wavelength remain essentially constant, because for d/L > 0.5 (deep water); the expression tanh
[2πd/L] approaches unity. Therefore, since the period remains constant, the celerity and wavelength also
do not vary. However, when a wave approaches the shallower water near the shore (where d/L <0.5),
Equations (2) and (3) cannot be simplified by ignoring tanh [2π/L]. From Equation (2), the celerity
decreases with depth; the wave slows as it enters shallower water. The same is true with the wavelength,
L, as can be seen from Equation (3), where it appears on both sides of the equation and an iterative
solution is required.
As the wave continues to move in shoaling water, its profile begins to steepen and its gently rolling
shape changes to a series of sharp crests with intervening flat troughs. At some point, this process can
continue no longer and the wave breaks at the shore. The break point is a function of the wave height;
period, water depth and bottom slope, but as a first approximation, assume that the wave breaks when the
height is about 0.78 times the depth. For example, a 5-foot high wave breaks in a water depth of about
6.4 feet.
Important wave properties are demonstrated when a train (series) of regular waves meets a solid
barrier such as an offshore breakwater,(Figure 2). Wave diffraction occurs when the waves pass the
breakwater and wave energy is transferred along their crests to the quiet area in the shadow of the
structure. This causes waves to form in the shadow zone that are smaller than in the adjacent unprotected
zone.
Wave reflection occurs on the offshore side of the breakwater. While waves passing the
structure are diffracted, the portions striking the breakwater are reflected like a billiard ball from a
7




 Previous Page
Previous Page
