^
where k is the approxi mate concentration defined by the expressions below from Bowers et al.( 2000)
using the mean resultant defined above:
^
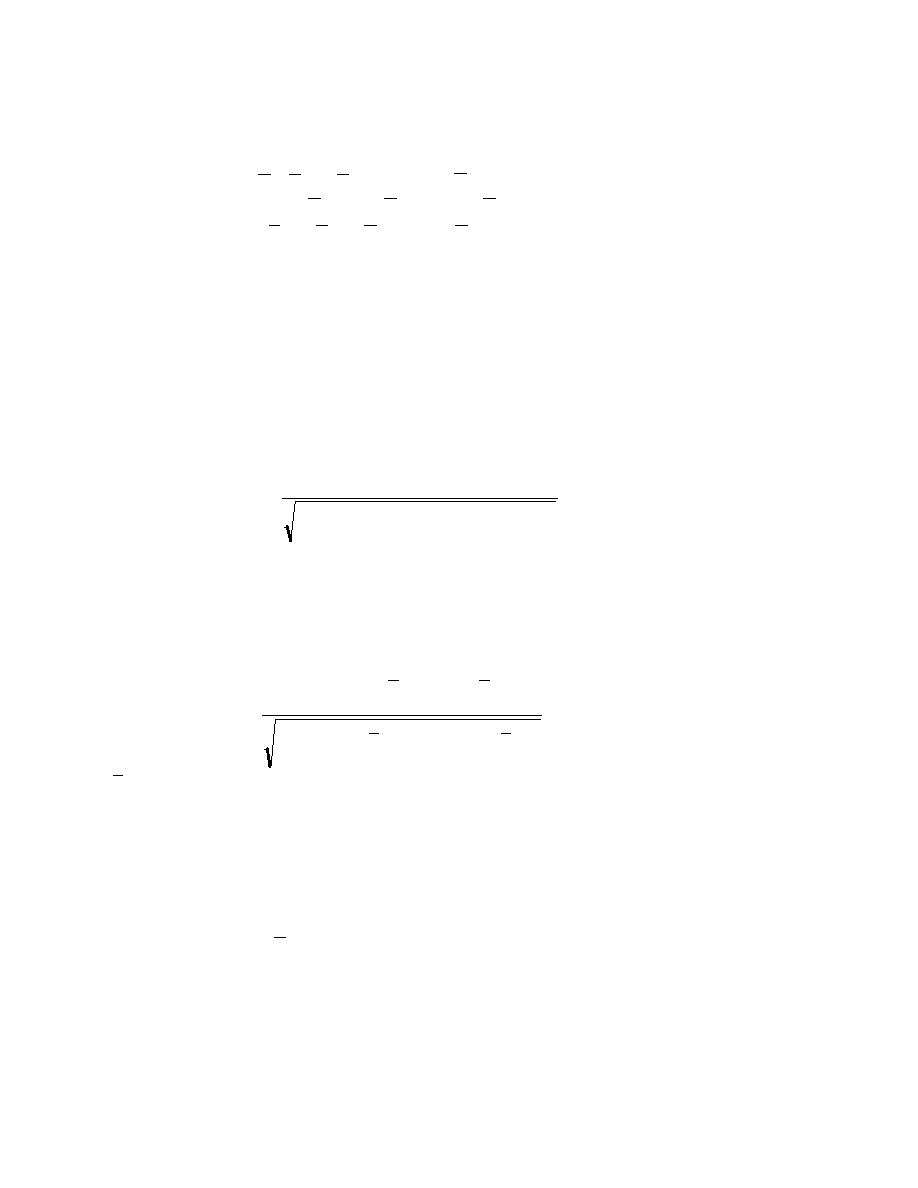
k = 2 R + R 3 + 5R 5 / 6
if R <0.53
^
k =-0.4+1.39 R +0.43(1- R )
if 0.53≤ R <0.85
(7)
^
k = 1/(R 3 - 4R 2 + 3R )
if R ≥0.85
The concentration statistic is a measure of the tightness of the distribution. If the concentration is >5.0,
the distribution is tightly grouped; lower concentration values indicate a distribution with more spread
Bowers et al.(2000).
Correlation statistics involving the two distributions are also helpful is defining whether the
measurement mean wave direction distribution and the WIS mean wave direction distribution are similar
for the month of data. This correlation in addition to the concentration statistic adds credibility to the
mean directional difference. The circular correlation defined in Bowers et al. (2000) and Fisher (1993)
was used in addition to an adaptation of the usual linear correlation coefficient, cor, defined in Johnson
and Wichern (1999). The circular correlation, circor, is defined by
∑ sin( x
- x j ) sin( yi - y j )
i
1≤i≤ j ≤n
circor =
(8)
∑
∑ sin
sin ( x i - x j )
( yi - y j )
2
2
1≤i≤ j≤ n
1≤i≤ j≤n
where x represents measurement directions and y represents WIS directions. The i and j subscripts refer
to the various hourly measurements that range from 1 to n. The linear correlation coefficient, cor, using
each distribution's mean directional difference was also used to give information on the relationship of the
two distributions. In this representation, sine functions of the angular differences were used rather than
just angular differences.
n
∑ sin(θ
- θ m ) sin(θ w - θ w )
m
cor =
i =1
(9)
n
n
∑ (sin(θ
- θ m )) 2 ∑ (sin(θ w -θ w )) 2
m
i=1
i=1
θ in Equation 9 is the mean direction corresponding to each of the distributions; the m subscript
corresponds to the measurement distribution and the w subscript corresponds to the WIS direction
distribution. Numerical values for circular correlation and linear correlation were very close with the
circular correlation sometimes being more sensitive and giving a slightly lower correlation estimate than
the linear statistic.
The mean resultant length defined above can be used to define the sample circular variance (Fisher,
1993), V, by
V = 1- R
(10)
The sample circular standard deviation is defined as (Fisher, 1993):
v = [- 2 log(1 - V )]
1/ 2
(11)
which can be approximated by




 Previous Page
Previous Page
