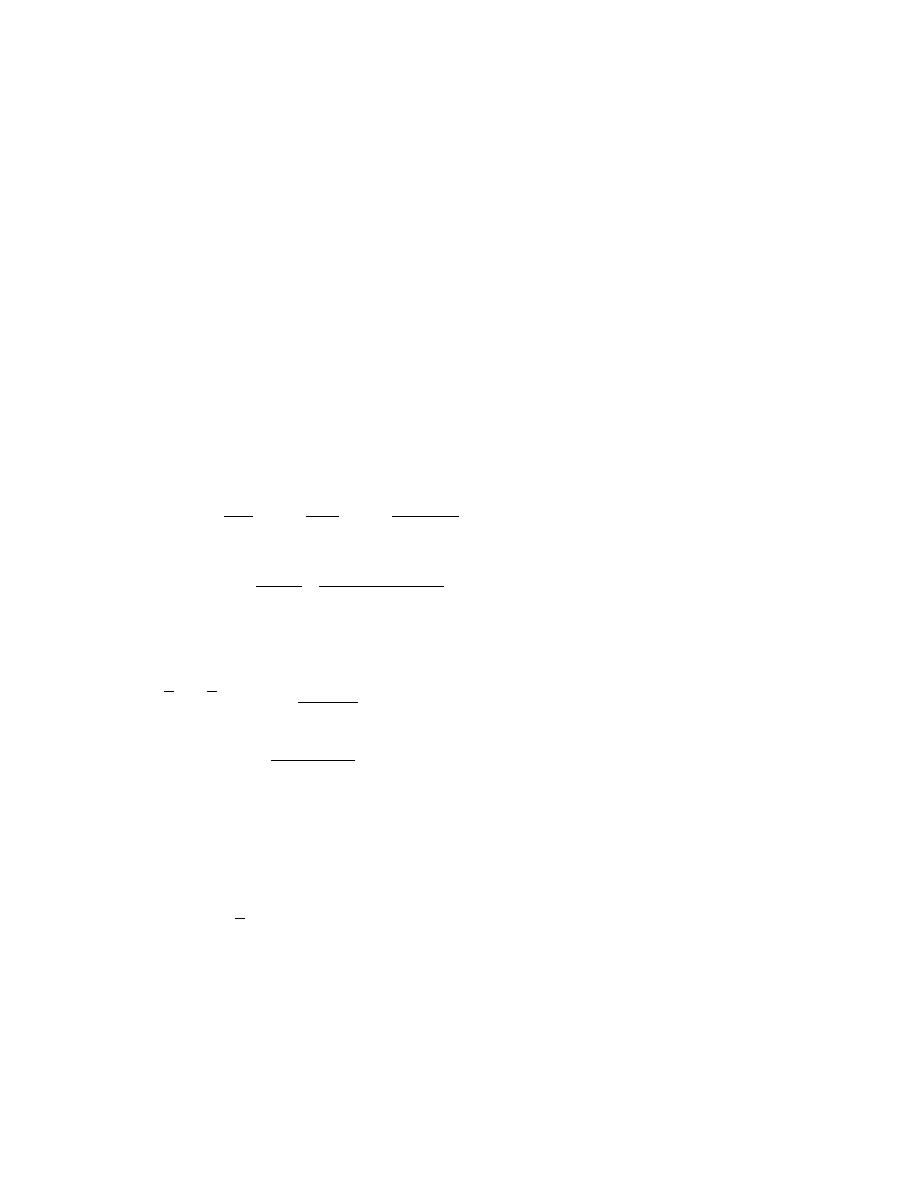
ERDC/CHL CHETN-III-64
June 2002 (revised)
determined to be depth limited from a shoaling/refraction/diffraction study. The design wave
height is calculated at a distance of 5Hs seaward from the structure toe.
Given design values:
Significant wave height: Hs = 2.07 m (6.8 ft)
Specific gravity of seawater: S = 1.0256
Specific gravity of armor stone: Sr = 2.65
Specific weight of armor stone: γr = 2.66x104 N/m3 (169.6 lb/ft3)
Density of armor stone: ρr = 2.72 t/m3 (5.27 slug/ft3)
Mean wave period: Tm = 10.8 s
Structure seaward slope: tan α = 0.5
Median stone size: W50 = 1,311 kg (2,889 lbs)
Storm duration: 4 hr = 14,400 s (1,333 waves at Tm)
Armor layer thickness: 2Dn50
Calculations:
1/ 3
1/ 3
1/ 3
W
M
1.311 t
Dn50 = 50
= 50
=
= 0.784m
γr
ρr
2.72 t/m3
Hs
2.07 m
Ns =
=
= 1.60
∆Dn50 (2.65 - 1)0.784 m
Damage due to a single storm would be computed using Equation 2 as
( Ns )5
(t 0.25 - tn.25 )
0
n
S (t ) = S (tn ) + 0.025
(Tm )0.25
n
1.605
(14, 400 s)0.25 = 1.58
= 0 + 0.025
(10.8 s)0.25
This damage level indicates that, for the single 4-hr storm, there would be an eroded area of
about 1.6 median-sized stones removed from a typical cross section. This is minimal damage and
would not affect the integrity of the structure. Assuming uniform wave height alongshore, the
alongshore variability, given as the standard deviation, of damage would be given by Equation 7.
0.65
= 0.5(1.58)0.65 = 0.67
σ S = 0.5 S
And the alongshore range of damage would be given by Equation 4 as
-2.7(0.67) + 1.58 ≤ S ≤ 3.0(0.67) + 1.58
S ≥0
0 ≤ S ≤ 3.61
6




 Previous Page
Previous Page
