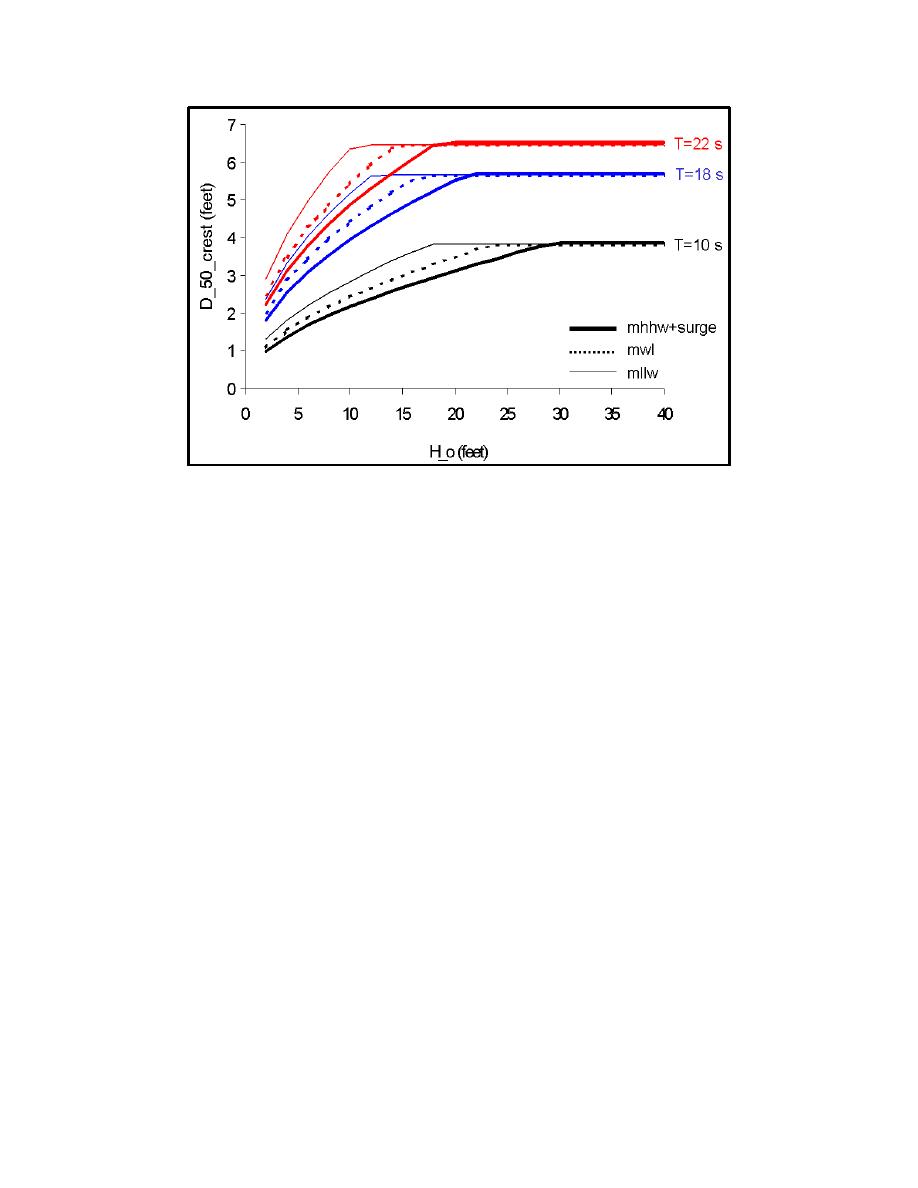
Figure A7.
Crest stone size for a submerged breakwater as a function of deep-
water wave height for a range of wave periods and water levels for
Ocean Shores (R=0.5, S=2) following van der Meer and Pilarczyk
(1990)
Vidal et al. (1992) and Vidal, Losada, and Mansard (1995) conducted
laboratory experiments to develop damage curves for various sectors of
submerged structures (e.g., front slope, crest, back slope, front head, and back
head). For each sector, damage curves relating the nondimensional freeboard, Rd
= R/D50, (where R = hc - h), with the stability number, Ns, for a given damage
level were obtained.
Vidal et al. (1992), Vidal, Losada, and Mansard (1995), Vidal, Medina, and
Martin (2000), and Rufin et al. (1994, 1996) show that the most critical location
for stability on submerged breakwaters is at the crown edge and backslope.
Backslope stability increases significantly with increasing submergence.
Based on results of these and other physical model experiments, Vidal,
Medina, and Martin (2000) developed a methodology and proposed a series of
equations based on Rd and Ns to assess stability and damage of submerged
structures. The procedure involves calculating the armor size, D∞, of a
conventional emergent rubble-mound breakwater with the same characteristics
(e.g., core, layers, slope, and damage level) by means of any available formula.
In this case, we have applied the well-known Hudson formula (SPM 1984) to
calculate D∞ for conventional emergent breakwater assuming a unit weight of
armor stone unit of 165 lb/cu ft. A value of 2 for Kd was deemed appropriate for
rough angular quarry stone, placed randomly and subject to breaking waves
(Shore Protection Manual 1984, Table 7-8). D∞ is then applied to scale the
freeboard (Rd∞ = R/D∞). The front slope armor unit size can be determined from:
A10
Appendix A
Stability Analysis of a Submerged Spur, North Jetty, Grays Harbor, WA




 Previous Page
Previous Page
