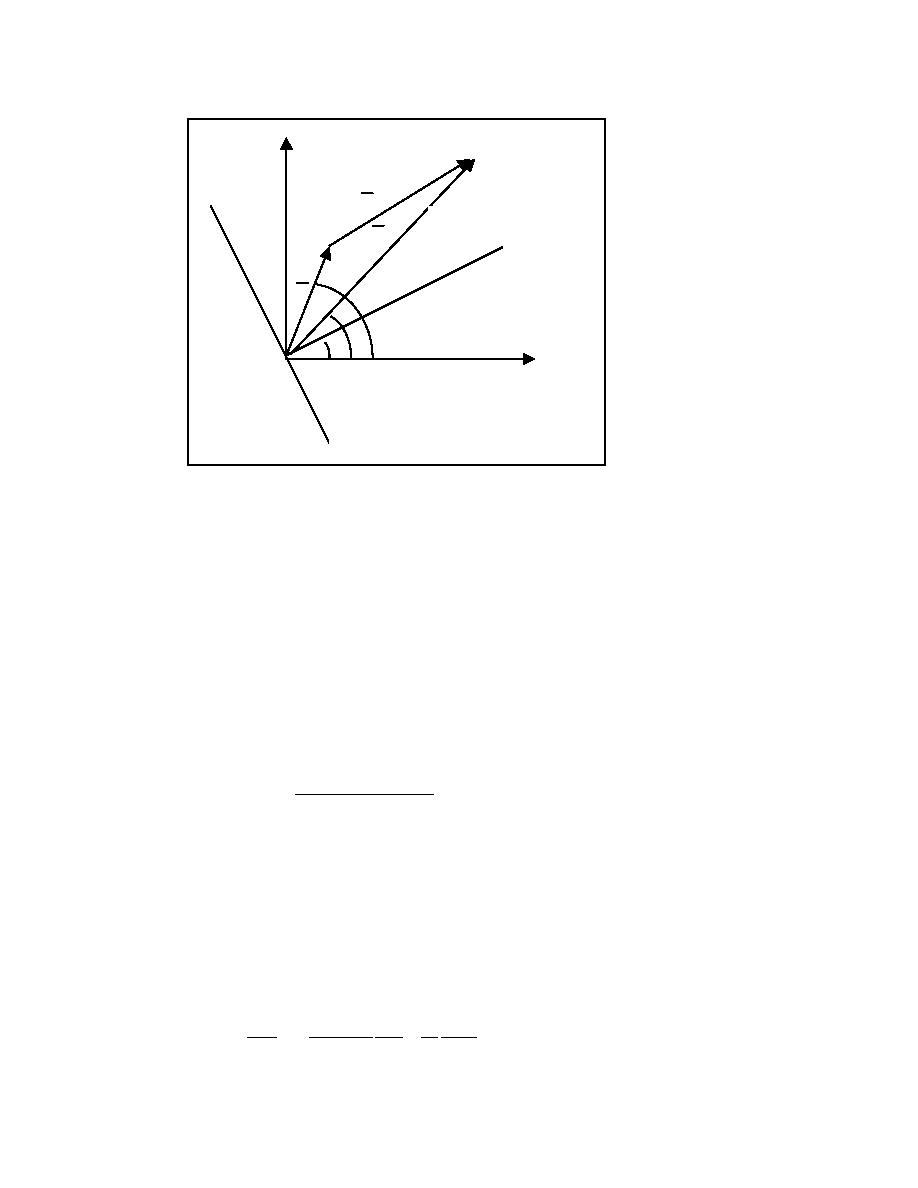
y
Cgr
ray
Cga
current
orthogonal
U
α δ
x
wave crest
Figure 2. Definition sketch of wave and current vectors
The direction of both the relative celerity and group celerity is α, the wave
orthogonal direction. In the absolute reference frame,
Ca = Cr + U cos(δ - α )
(5)
(C ga )i = (Cgr )i + (U )i
(6)
where subscript i is tensor notation for the x- and y-components. The direction of
the absolute celerity is also in the wave orthogonal direction. The absolute group
celerity defines the direction of the wave ray, so the wave ray direction (Figure 2)
is defined as:
Cgr sin α + U sin δ
= tan -1
(7)
Cgr cosα + U cosδ
The distinction between the wave orthogonal (direction perpendicular to the
wave crest) and the wave ray (direction of energy propagation) is important in
describing wave-current interaction. Without currents, the wave rays and
orthogonals are the same, but with currents, the wave energy moves along the
rays whereas the wave direction is defined by the orthogonals.
The wave orthogonal direction for steady-state conditions is given by (Mei
1989; Jonsson 1990):
Dα
Cr k Dd ki DU i
=-
-
Cga
(8)
DR
sinh 2kd Dn k Dn
7
Chapter 2 Governing Equations and Numerical Discretization




 Previous Page
Previous Page
