How will the blanket be stabilized at the toe of the bank
How will the blanket be tied into the bank at its upstream and downstream ends
6.5.2 Stability Factor Design Methods
Stability Factors For Riprap. In the absence of waves and seepage, the stability of rock riprap
particles on a side slope is a function of: (1) the magnitude and direction of the stream velocity
in the vicinity of the particles; (2) the angle of the side slope; and (3) the characteristics of the
rock including the geometry, angularity and density. The functional relations between the
variables are developed below. This development closely follows that given by Stevens and
Simons (1971).
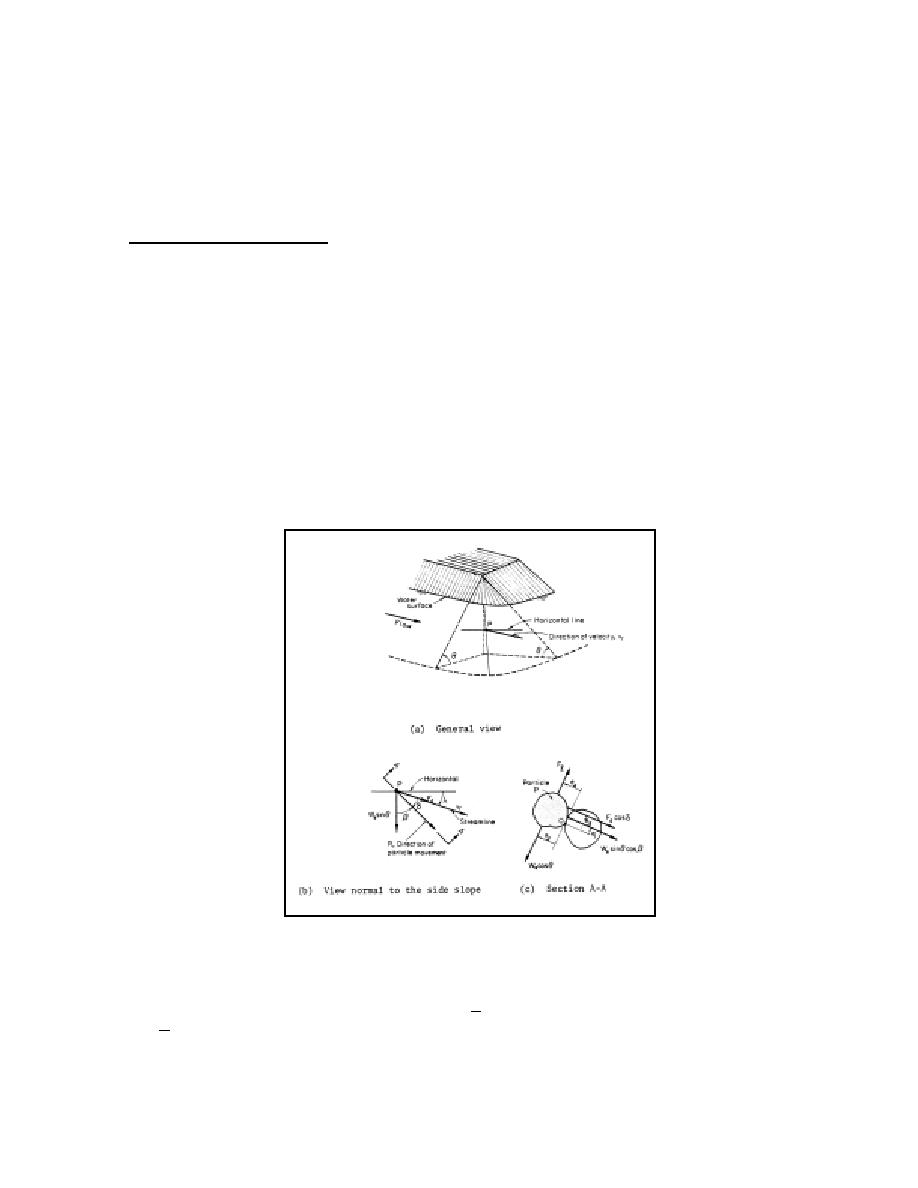
Consider flow along an embankment as shown in Figure 6.13. The fluid forces on a rock
particle identified as P in Figure 6.13a result primarily from fluid pressure around the surface of
the particles. The lift force F4 is defined herein as the fluid force normal to the plane of the
embankment. The lift force is zero when the fluid velocity is zero. The drag force Fd is defined
as the fluid force acting on the particle in the direction of the velocity field in the vicinity of the
particle. The drag force is normal to the lift force and is zero when the fluid velocity is zero.
The remaining force is the submerged weight of the rock particle Ws.
Figure 6.13. Diagram for riprap stability conditions.
Rock particles on side slopes tend to roll rather than slide, so it is appropriate to consider the
stability of rock particles in terms of moments about the point of rotation. In Figure 6.13b the
direction of movement is defined by the vector R . The point of contact about which rotation in
the R direction occurs is identified as point "0" in Figure 6.13c.
6.21




 Previous Page
Previous Page
