=
0.77∆, if ∆/δ′ > 1.8
(4.36a)
X
=
01.39δ′, if ∆/δ′ < 1.8
(4.36b)
X
∆
=
Apparent roughness of the bed, k s / X
X
=
Correction factor in the logarithmic velocity distribution equation given
as a function of k s / δ′ in Figure 4.7
= 11.6ν / V*′
δ′
(4.37)
= Einstein's velocity distribution equation = 5.75 log (30.2y / ∆)
′
(4.38a)
v / V*
V*′
= Shear velocity due to grain roughness = gR′ S
(4.38b)
b
R′
= Hydraulic radius of the bed due to grain roughness = R b - R′′
b
b
R′′
= Hydraulic radius of the bed due to channel irregularities
b
= Slope of the energy grade line normally taken as the slope of the
Sf
water surface
= Another correction term given as a function of D 65 / δ′ in Figure 4.8
Y
= log (10.6X / ∆)
βx
Z
E Z-1
1 - y
1
I1 = 0.216
(4.39)
dy
E
Z
y
(1 - E)
Z
E Z-1
1 - y
1
I2 = 0.216
(4.40)
In ydy
E
Z
y
(1 - E)
where:
ω / β κV*′ = ω / 0.4V*
′
Z
=
(4.41)
ω
=
Fall velocity of the particle of size Ds
E
=
Ratio of bed layer thickness to flow depth, a/yo
yo
=
Depth of flow
a
=
Thickness of the bed layer, 2D65
The two integrals I1 and I2 are given in Figures 4.9 and 4.10 as a function of z and E.
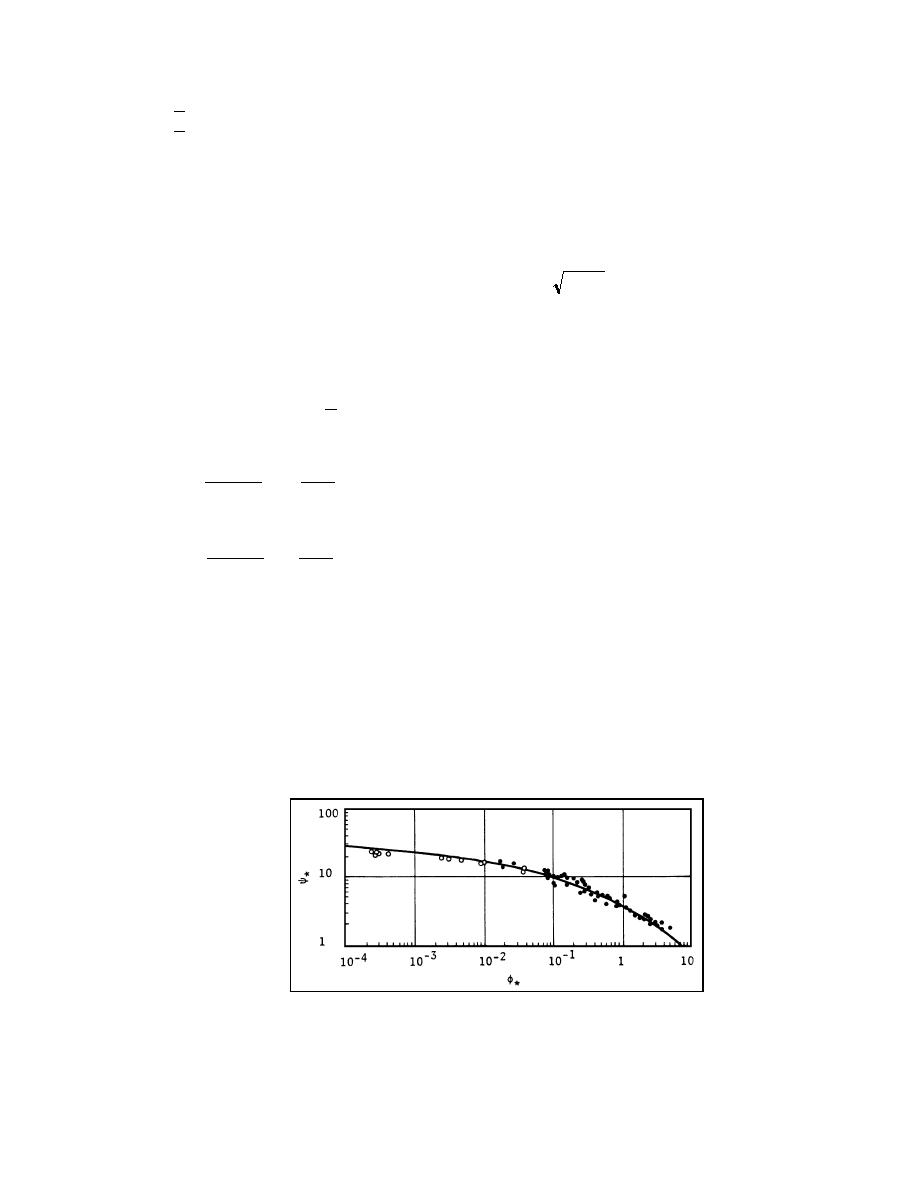
Figure 4.5. Einstein's φ* vs ψ * bed load function (Einstein 1950).
4.15




 Previous Page
Previous Page
