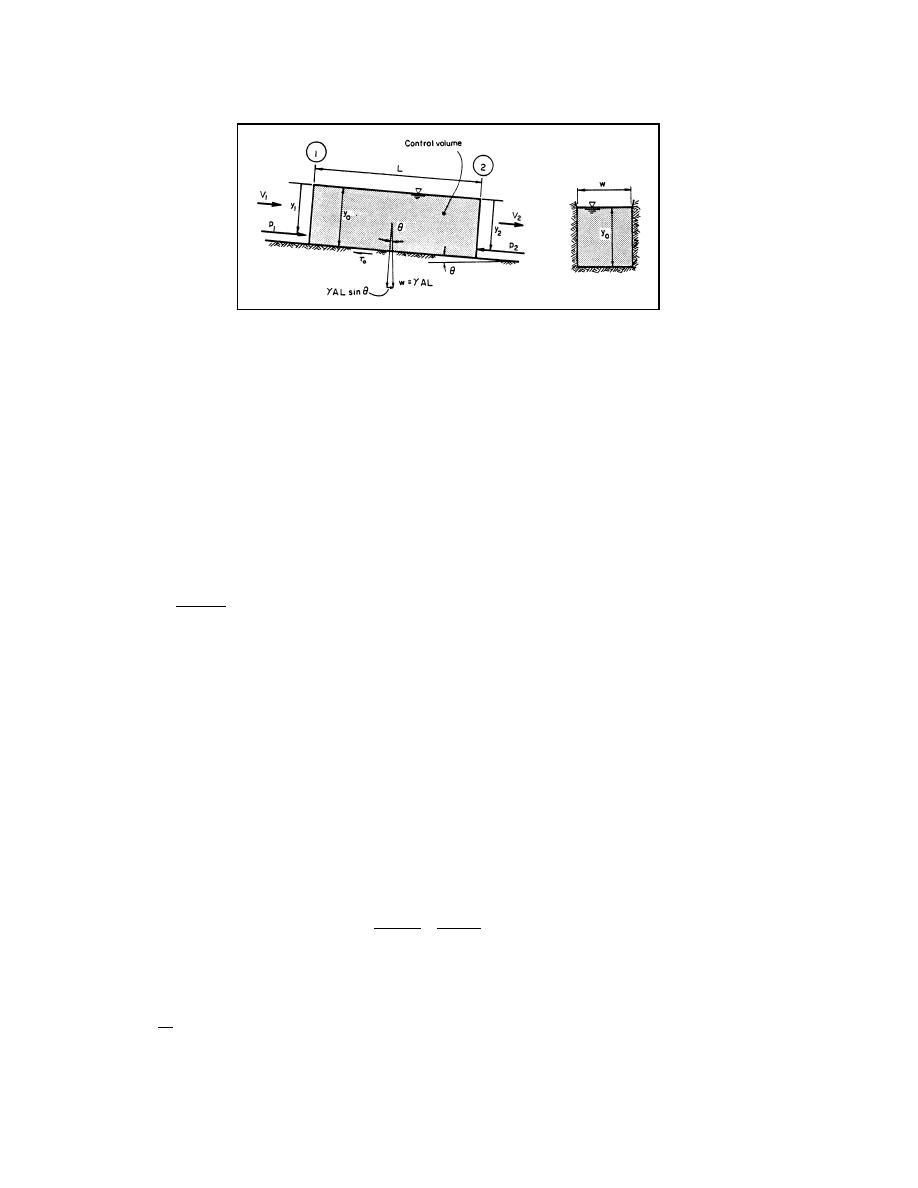
Figure 2.11. Control volume for steady uniform flow.
ρy o WV2 - ρy o WV1 = 0
(2.87)
or
V1 = V2
(2.88)
The conservation of momentum in the downstream direction is described from Equation 2.25 with
A1 = A2 = Wyo and V1 = V2. The pressure forces acting on the control boundary are approximated
by:
γ yo W
2
F1 = F2 =
(2.89)
2
The downstream component of the body force γAL (equal to the weight of fluid in the control
volume) in the X direction is:
Fb = γAL sin θ
(2.90)
where θ is the slope angle of the channel bed. The average boundary shear stress is τo acting
on the wetted perimeter P. The shear force Fs in the x-direction is:
Fs = τo PL
(2.91)
With the above expressions for the components, the statement of conservation of linear
momentum becomes:
γy o W γy o W
2
2
ρβ Wy o V - ρβ Wy o V = γAL sin θ +
-
- τo PL
2
2
(2.92)
2
2
which reduces to
A
τo = γ
sin θ
(2.93)
P
2.26




 Previous Page
Previous Page
