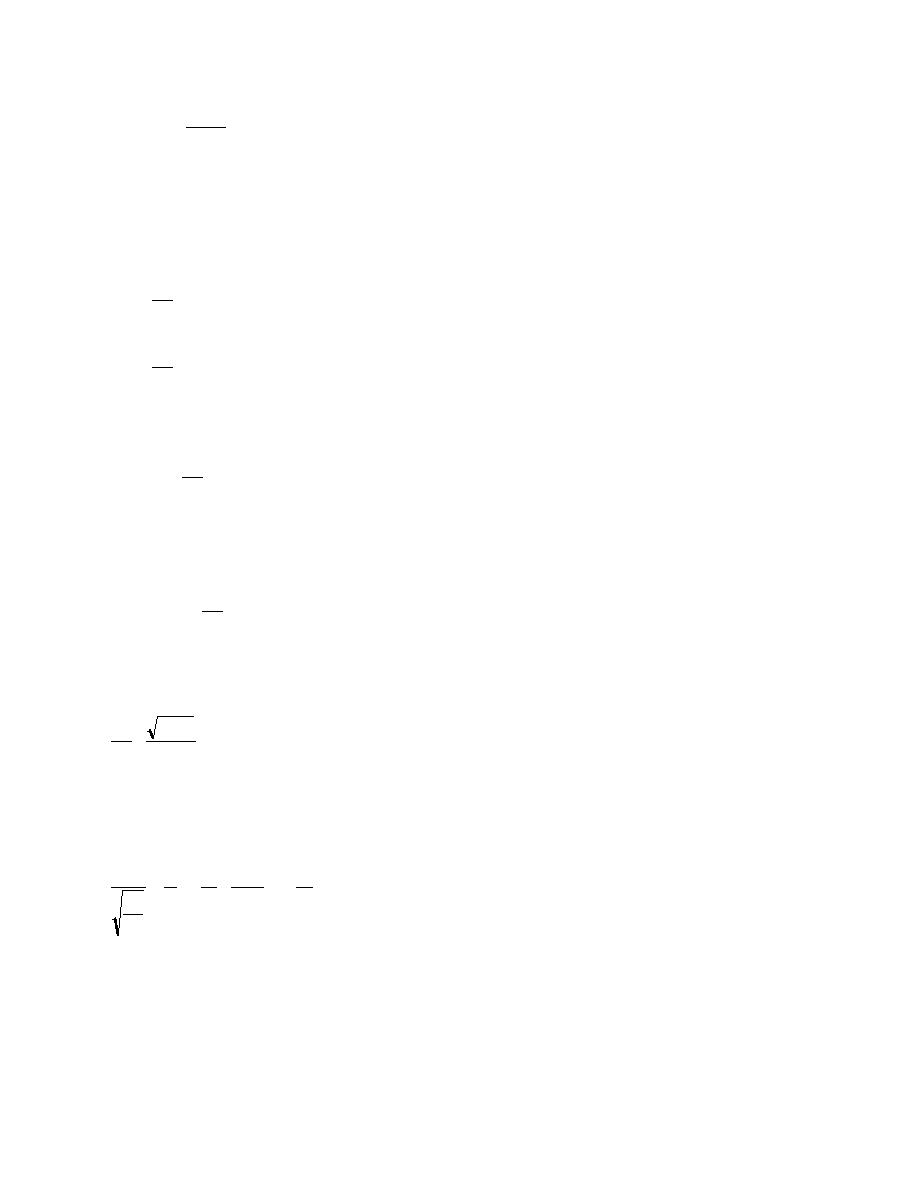
The term v ′x v ′y is the time-average of the product of v ′x and v ′y at a point in the flow. It is
called the Reynolds shear stress.
Prandtl (1925) suggested that v ′x and v ′y are related to the velocity gradient dv/dy shown in
Figure 2.9b. He proposed to characterize the turbulence with a dimension called the "mixing
length" l, which is assumed to be the same in both the x and y directions. Accordingly,
dv
v ′x ~ l
(2.70)
dy
dv
v ′y ~ l
(2.71)
dy
and
2
dv
τ ~ ρ l2
dy
(2.72)
If it is assumed that the mixing length can be represented by the product of a constant κ and y
(i.e., l = κy), then for steady uniform turbulent flow,
2
dv
τ = ρκ y
dy
2
2
(2.73)
Using different reasoning von Karman (1930) derived the same equation. Equation 2.73 can be
rearranged to the form:
τo / ρ
dv
=
(2.74)
κy
dy
where κ is the von Karman universal velocity coefficient. For rigid boundaries κ has the average
value of 0.4. The term τo is the bed shear stress. The term (τo/ρ)1/2 has the dimensions of
y
y 2.31
v
1
In =
=
(2.75)
log
y′
y′
κ
κ
τo
ρ
Here In is the logarithm to the base e and log is the logarithm to the base 10. The term y′ results
from evaluation of the constant of integration assuming v = 0 at some distance y′ above the bed.
The term y′ depends on the flow and has been experimentally determined. The many
experiments have resulted in characterizing turbulent flow into three general types:
2.18




 Previous Page
Previous Page
