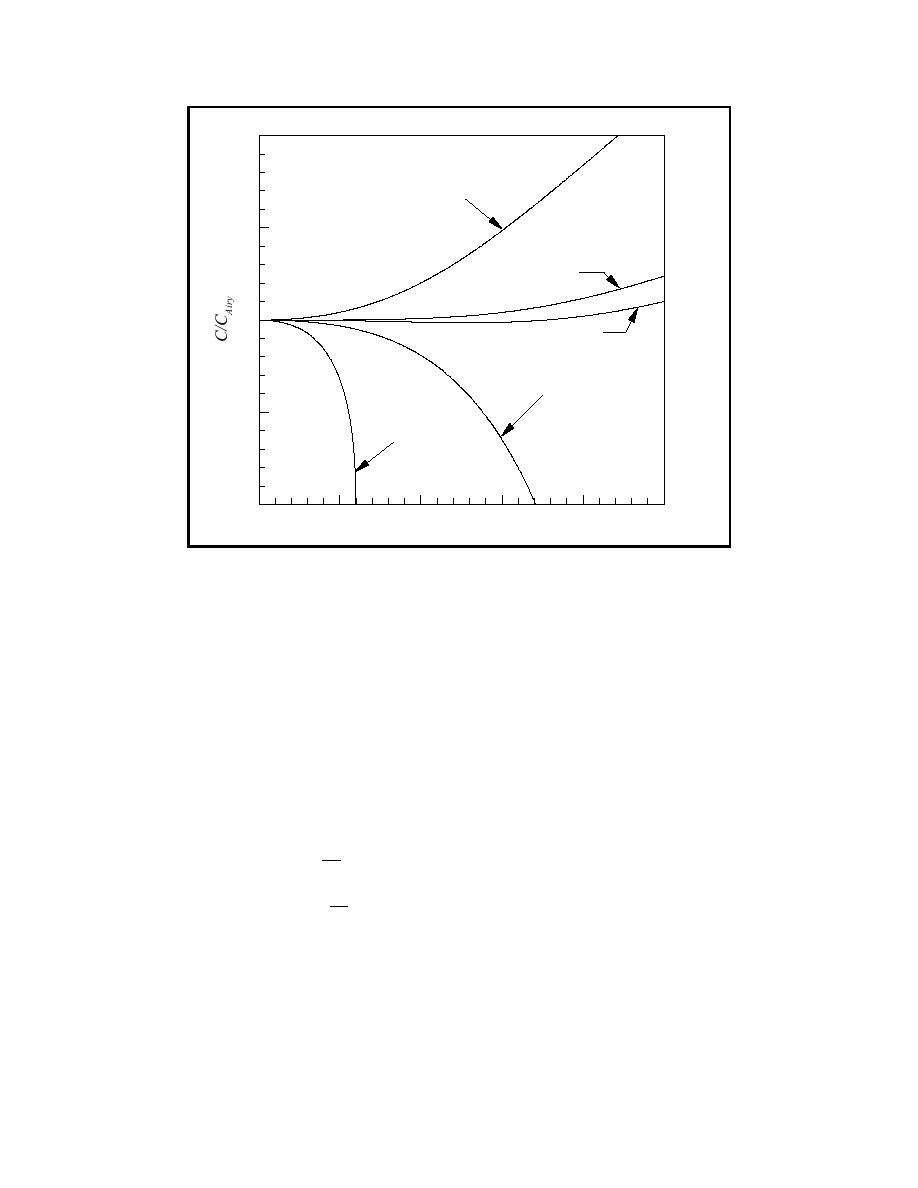
1.2
Bottom Velocity (α = -1/2)
1.1
Pade (2,2) (α = -2/5)
1
Modified Pade
(α = -0.392)
Depth-Averaged Velocity
(α = -1/3)
0.9
Velocity at Free Surface
(α = 0)
0.8
0.1
0.2
0.3
0.4
0.5
h/Lo
Comparison of normalized phase speeds for different values of α
Figure 1
wave train consisting of two small amplitude periodic waves with amplitudes, a1
and a2, frequencies, ω1 and ω2, wave numbers, k1 and k2, and propagating in
directions θ1 and θ2 respectively. The water-surface elevation can be written as:
η(1) ( x, t) = a1 cos(k1 ⋅ x - ω1t) + a2 cos(k2 ⋅ x - ω2t)
(11)
where k = (kcosθ, ksinθ). The second-order wave will consist of a subharmonic
quencies 2ω1, 2ω2 and ω+ = ω1 + ω2. This can be written as:
a12
η ( x, t ) =
G+ (ω1 , ω1 , θ1 , θ1 ) (cos(2k1 ⋅ x - 2ω1t)
(2)
2
2
a2
+
G+ (ω2 , ω2 , θ2 , θ2 ) cos(2k2 ⋅ x - 2ω2t)
(12)
2
+ a1a2G (ω1, ω2 , θ1 , θ2 ) cos(2k ⋅ x - 2ωt)
where k = k1 k2, and G(ω1, ω2, θ1,θ2) is a bidirectional quadratic transfer func-
tion that relates the amplitude of the second-order waves to the amplitude of the
first-order waves. Dean and Sharma (1981) derived expressions for the bidirec-
tional quadratic transfer function based on second-order Stokes theory. Nwogu
7
Chapter 2 Theoretical Background





 Previous Page
Previous Page
