8
Stokes (Superharmonic)
Boussinesq (Superharmonic)
Stokes (Subharmonic)
Boussinesq (Subharmonic)
6
4
2
0
0
0.1
0.2
0.3
0.4
0.5
h/Lo
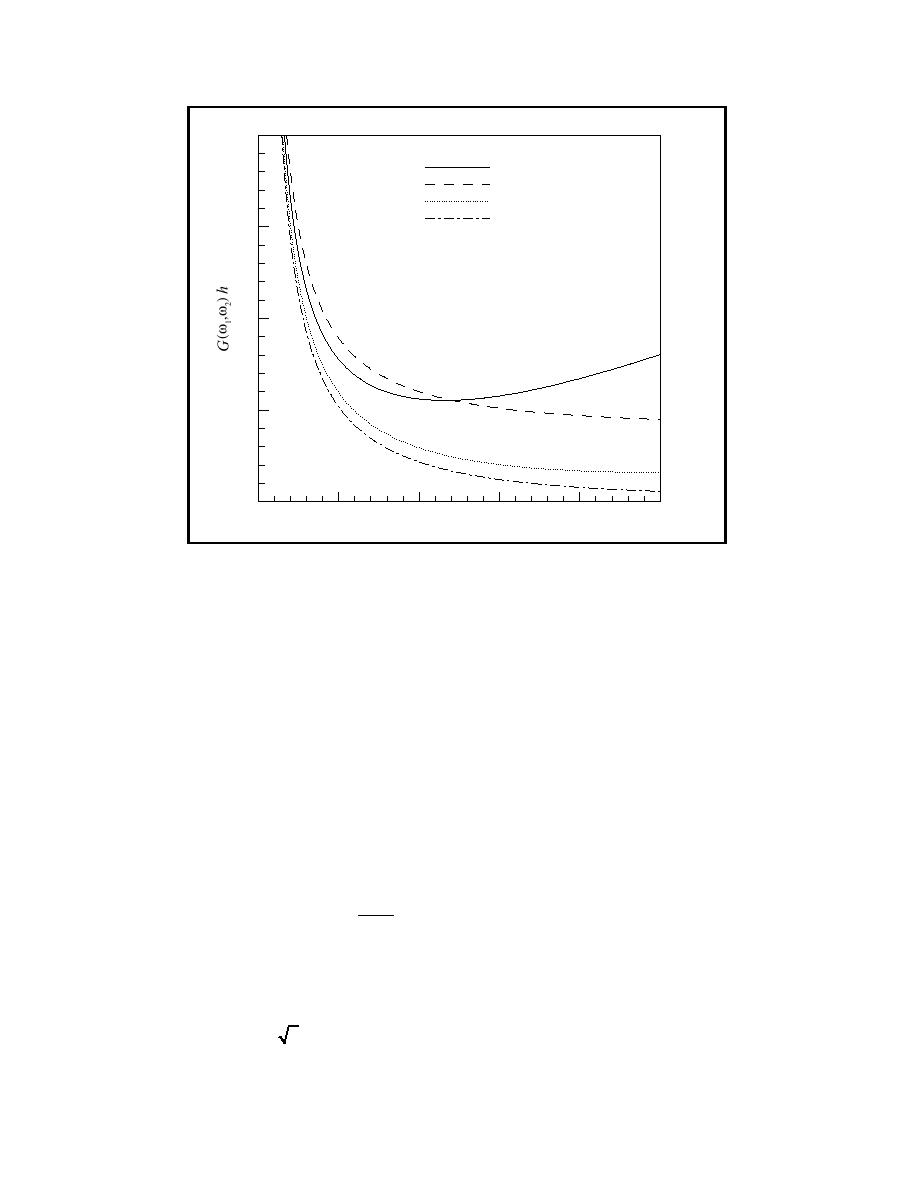
Figure 2.
Comparison of quadratic transfer function for Boussinesq and Stokes
theories
The effect of wave energy dissipation due to breaking is simulated in the
Boussinesq model by introducing an eddy viscosity term to the right-hand side of
the momentum equation (Equation 5 or 8). Nwogu (1996) used a dissipative term
of the following form:
=
- νt ∇(∇.uα )
Fbreaking
(15)
where νt is the turbulent eddy viscosity. As pointed out by Kennedy et al. (2000),
it is important for the dissipative term to dissipate energy but conserve momen-
tum to accurately capture details of the mean flow field associated with breaking
waves. A modified form of the dissipative term that ensures that momentum is
conserved can be written as:
1
∇{νt (h + η)∇ ⋅ uα }
=
-
Fbreaking
(16)
h+η
The eddy viscosity is determined from the amount of turbulent kinetic energy, k,
produced by wave breaking, and a turbulence length scale, lt, using:
νt = k lt
(17)
9
Chapter 2 Theoretical Background





 Previous Page
Previous Page
