ERDC TN-DOER-T6
September 2004
subtracting light ship displacement (weight) from loaded ship displacement, has the largest effect
of the four variables in the TDS equation. As would be expected, if the hopper weight is over-
estimated, the TDS value is likewise inflated, but when the hopper volume value is over-
estimated, the TDS value is calculated below its "true" value.
Besides impacts on measurements being caused by the water density inside the hopper, the
density of water surrounding the vessel can also impact TDS accuracy because of its influence
on the vessel's draft and respective displacement. The magnitude of this impact depends on
whether this error is systemic or random in nature.
TDS Measurement Uncertainty. Each measurement and physical quantity associated with
the calculation of dredging quantities has some error or uncertainty associated with it. The
equation for calculating TDS production is a function of multiple variables (measurements and
physical quantities), each contributing some error. These errors propagate through the data
reduction equation to the final calculation. It is essential that the error associated with each
variable is accounted for, and that the individual error contribution to the total error is
recognized. Equations are introduced in Scott (2000) that describe production for both pipeline
and hopper dredges. An uncertainty analysis expression is derived for each equation. Scott
applies the general uncertainty analysis technique in a step-by-step manner to show the
derivation of the uncertainty analysis expression. Example dredging situations are introduced in
Scott (2000) to demonstrate the uncertainty analysis application. Numerical solutions show the
error contribution of each variable, and the effect of uncalibrated instruments and unmeasured
sediment and water properties on the accuracy of production calculations.
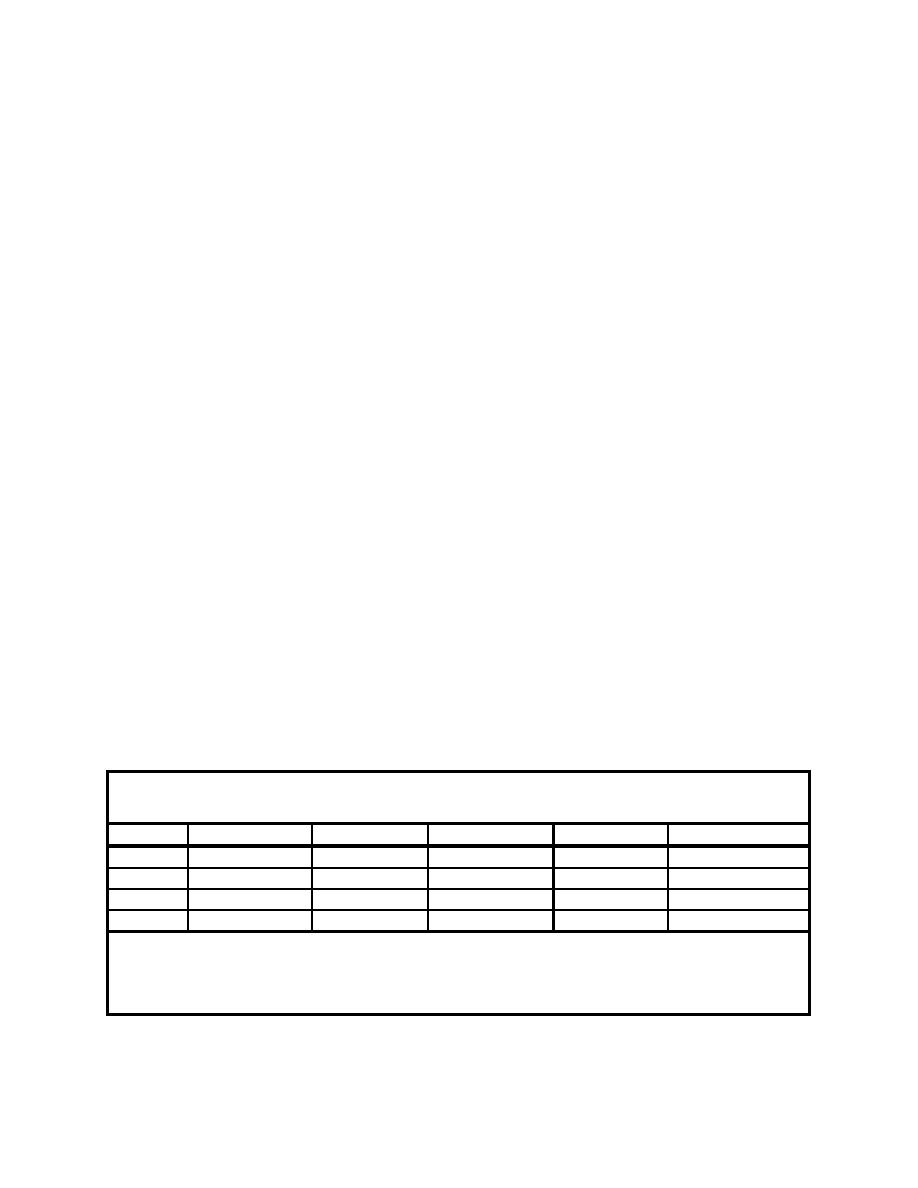
The results of Scott's example uncertainty calculations for TDS (Table 1) show that the error
potential is greatest for the case of poorly calibrated instruments (40 percent for Case 3), because
the average density measured in the hopper is dependent on two measured variables. The water
density contributes significant error when the instruments are properly calibrated. The error in
hopper production calculations ranged from a low of about 10 percent for calibrated instruments
and known sediment and water properties (Case 1), to over 40 percent for a worst case of
uncalibrated instruments and unknown material properties (Case 4) (Scott 2000).
Table 1
Example Hopper Dredge Uncertainty Calculations1
Case
Mineral Density
Water Density
Hopper Volume
Hopper Weight
Total Uncertainty
2
1
0.05
2.15
2.78
4.00
8.98
23
0.22
11.26
1.62
2.33
15.43
34
0.01
0.49
15.90
22.90
39.30
5
4
0.08
4.21
15.15
21.81
41.25
1
Information taken from Scott (2000). Percent uncertainty contributed by variable to total.
2
Case 1 - All instruments calibrated and sediment properties measured.
3
Case 2 - All instruments calibrated and sediment properties estimated.
4
Case 3 - Instruments out of calibration and sediment properties measured.
5
Case 4 - Instruments out of calibration and sediment properties estimated.
Scott presents this example only as a guide for applying the uncertainty analysis method for
determining the accuracy of this type of production system calculation. It should be apparent
13




 Previous Page
Previous Page
