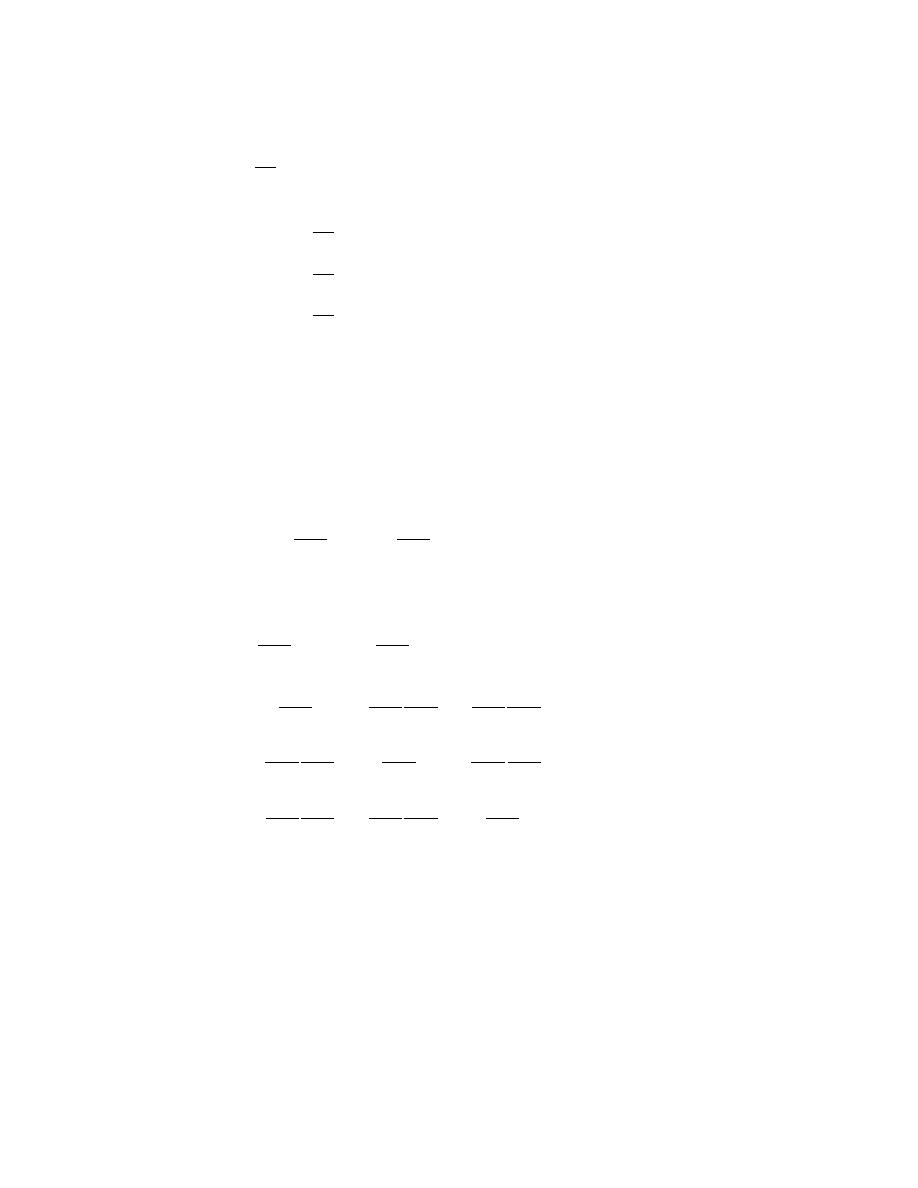
Note that for future use, we give
∆e
∫ N dx dy = 3
∫
e
m
e
6 e
60 ∆ , i = j = k
2 e
∫e∫
∫
N i N j N k dx dy = ∆ , i = j or i = k or j = k
e
e
e
60
1 ∆e , i ≠ j ≠ k
60
Notice that in the above formulations, (i, j, k) are denoted in a counter-clockwise manner.
For element e, the following relations can be established for substitution into (19):
r 3 e Ne r 3 e Ne
∇ η = i ∑ ηi
+ j ∑ ηi
e
i
i
$
$
$
(24)
x
y
i=1
i =1
(
)
2
∇ ηe
= ∇ ηe ⋅∇ ηe
$
$
$
2
2
3 e Ne 3 e Ne
= ∑ ηi
+ ∑ ηi
i
i
$
$
y
x i=1
i =1
N e 2
N1 N e N1 N 3
e
e
e
1
2
xa
x a x a x a x a
N e N 3 e
e
2
N 2 N1
Ne
e
e
{}
{}
e T
η
= η
2
2
$
$
x a x a
x a x a
xa
2
N 3 N1
N3 Ne
Ne
e
e
e
x a x a
3
2
xa xa
xa
(25)
and
15
Previous Page
