As for non -isotropic cases there is an additional possibility to estimate not only the first Kolmogorov constant, but
also the second one using (21). The corresponding results are presented in Table 1
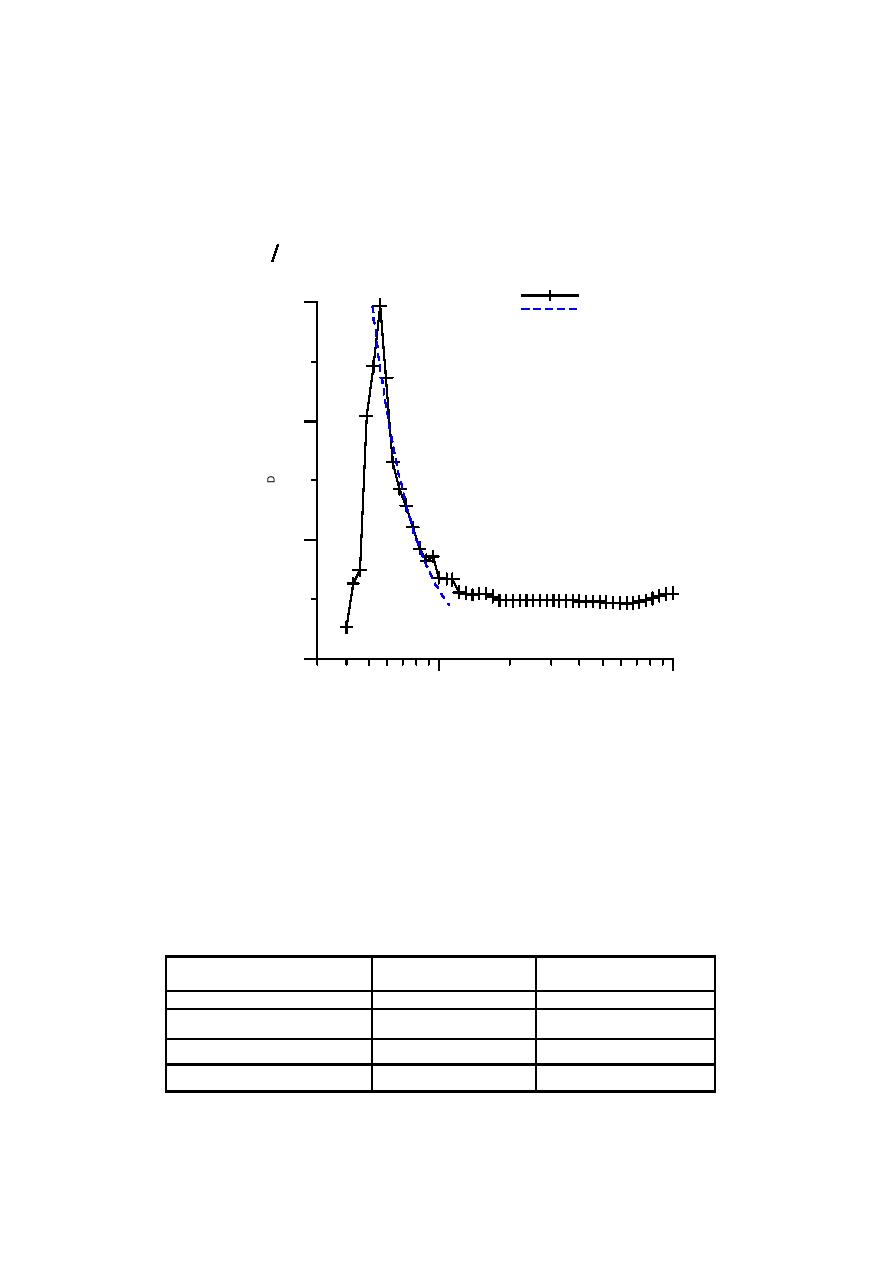
An angular spectrum width D (Fig.7) can be determined as a proportion of the frequency-angular spectrum value at
the main direction to the frequency spectrum as follows:
D(ω) = S (ω, β p ) S (ω)
(25)
D
1
1.2
2
0.8
0.4
0
ω, rad/s
1
10
Frequency (rad/s)
Fig. 6
Function D(ω)
1- numerical results; 2 - local approximation: D ≈ 0.235 ⋅ ω-2.4
ω = 0.5 0.6 rad/s. After
The function D is shown in Fig. 6. Its maximum value is achieved at the frequencies
that it is quickly reduced as soon as the frequency is increased, showing that the function of angular energy
distribution becomes wider.
Final estimation results of the Kolmogorov constants for different values of external angular functions are presented
in Table 1. As it is seen the estimations of the first and the second constants are varied weakly depending on the
external angular function distribution.
ESTIMATION OF KOLMOGOROV CONSTANTS FOR DIFFERENT ANGULAR DISTRIBUTION FUNCT IONS
TABLE1
α0
Angular function distribution
α1
of energy generating force
0.303 0.033
Isotropic
0.308 0.020
0.218 0.015
cos (β /2)
0.324 0.021
0.239 0.023
cos 2 (β)
0.311 0.023
0.242 0.034
cos4 (β)




 Previous Page
Previous Page
