Figure 4. ∆q versus ∆t computed using ISSDOT for stated conditions change in volume used to compute ∆q for each ∆t is also shown

Figure 3. ∆q versus ∆t as computed using ISSDOT for stated conditions

Figure 5. ∆q versus ∆t computed using ISSDOT for stated conditions

chetn-vii-5
Page Navigation
6

Power (t4-TPD-1sf-grid)

200

Power (t2-TPD-1sf-grid)

400

150

300

Note: Line for Trip 2 is extrapolated left of the data points by a power

∆t in hours

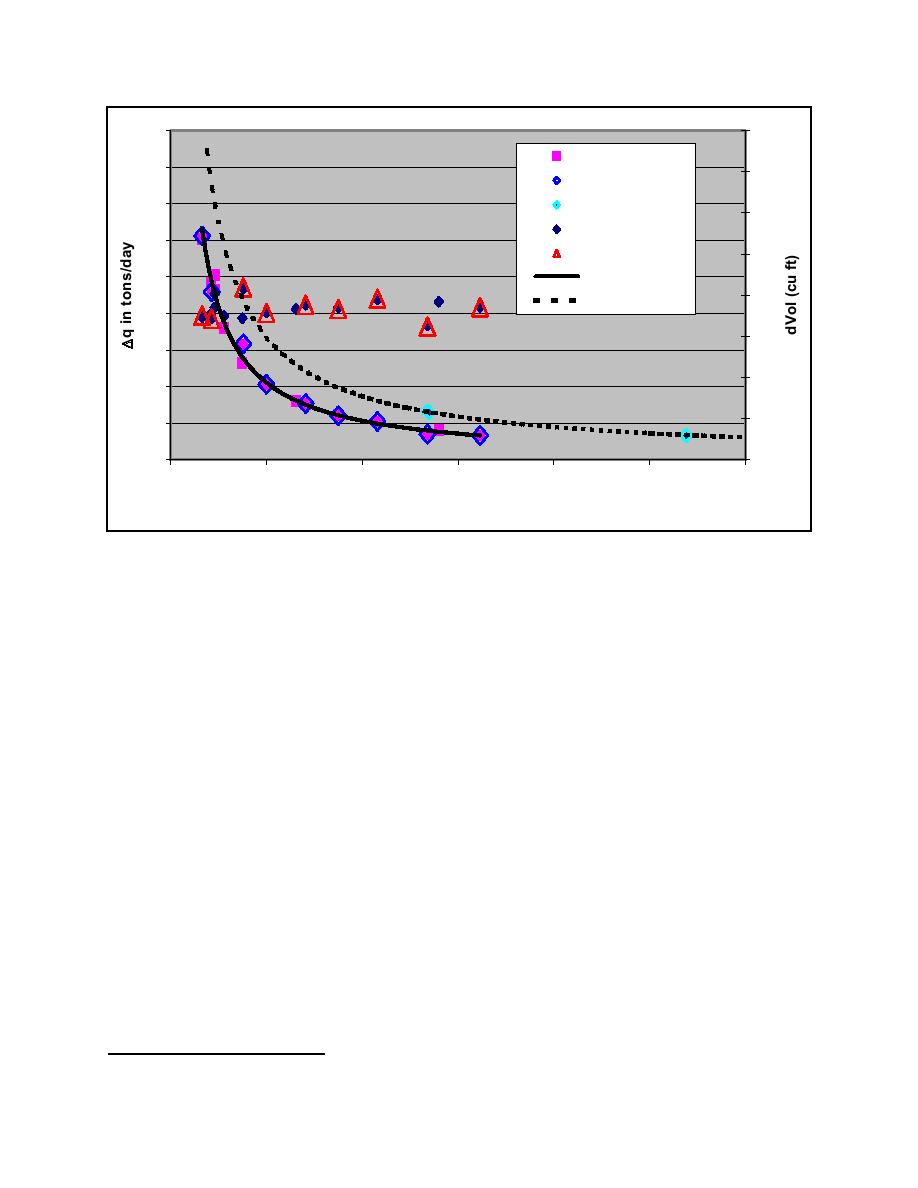
Figure 4. ∆q versus ∆t computed using ISSDOT for stated conditions change in volume used to compute

∆q for each ∆t is also shown (Tons/day vs. time span between measurement of two sections.

Average of 30 rows at each ∆t. Data from trip 4 and 2)

In the legend the first line means trip 4 ∆q in tons per day for a 1-sq ft grid.1 All lines in the legend

use this same convention. One- and four-sq ft grids were used for the computations to check the

method's spatial sensitivity. For these data and those two grid sizes, there wasn't much difference in

the computational results. Considering the plotted values, the two data points for trip 2 data between

the 2.5- and 3-hr time spans fall clearly above the data trend for the trip 4 data. Since both data sets

were taken at nearly identical flow rates, one could propose that the trip 2 data points do in fact

indicate an increase in bed-load mobilization due to the drawdown. However, two data points are

insufficient to assert any statistical significance. But, these data taken together with other relevant

data and analysis could make a strong case for the increase of bed-load mobilization due to the

drawdown. Towards this goal, something needs to be said regarding the ISSDOT method of

computing bed-load transport, since it was used to arrive at the data plotted in Figures 3 and 4.

The ISSDOT method is new and still in a development stage. So far, the preliminary results of field

tests and a flume study indicate that the method is capable of determining the bed-load transport

gradient (∆q) on large sand bed rivers. This is of course subject to certain limitations. As stated

earlier, at the present time it cannot be said that the method provides a quantitative value for the true

bed-load transport rate of a large river. However, given the way the data are collected and analyzed,

it does appear to be able to quantify relative differences of transport gradients at a given location.

The reason for this is the quality and repeatability of the collected data, as well as the consistency in

To convert to kilograms per square meter, multiply number of tons by 9,764.856.

Index

Privacy Statement
Press Release
Contact