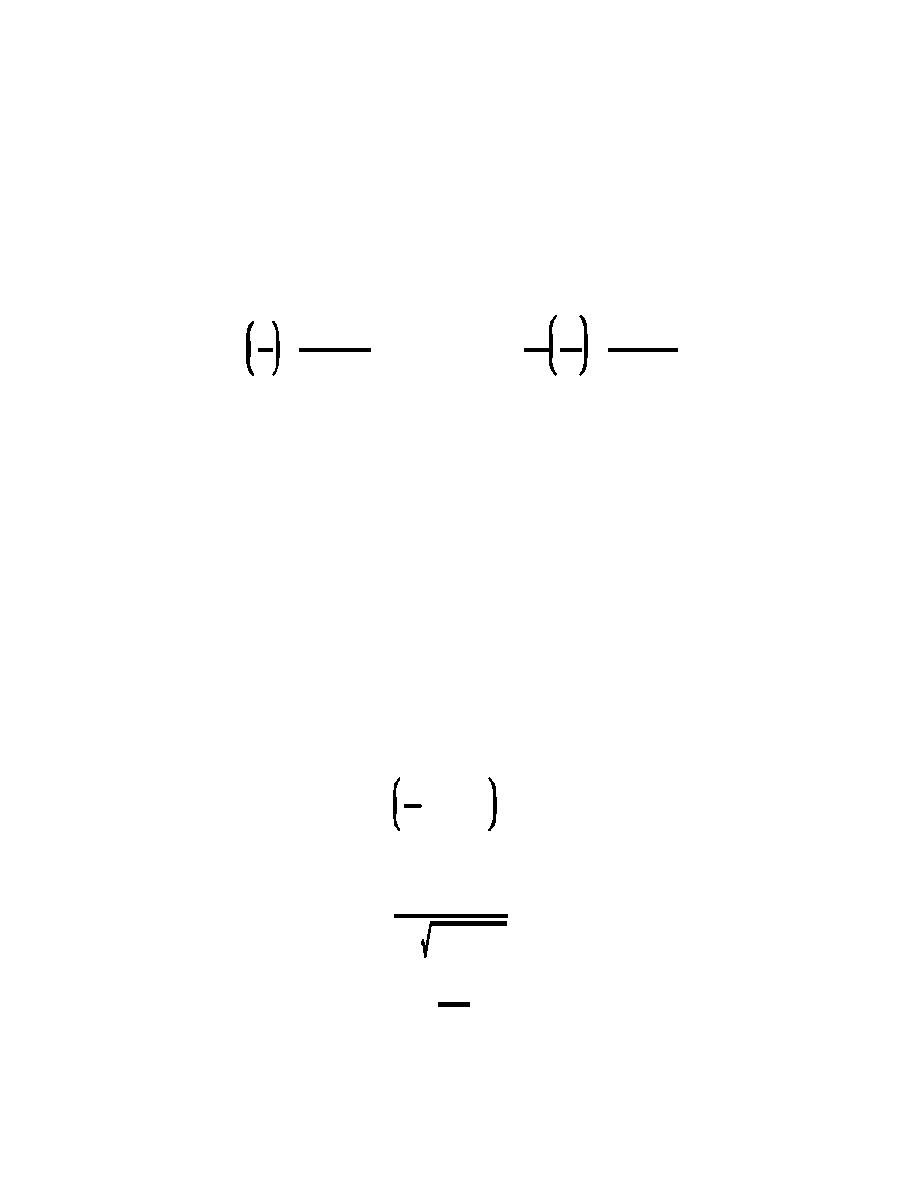
Fundamentals of Engineering Design
Gravel river beds typically have a large distribution of particle sizes. Bed material will be
transported at variable depths in the water column depending on the size of the particle and hydraulic
characteristics of the flow. When gravel is being considered, there is typically two classifications of
sediment discharge. Bedload refers to the portion moving on or near the bed of the river. Total load is
defined as the total amount of sediment being transported (Biedenharn et al., 1997). The total load is
comprised of the bedload and the portion being transported in suspension.
A dimensionless equation for the calculation of bedload discharge capacity was developed by
Meyer-Peter and Mller (1948):
Qp n ) 3/2 (RS f
1/3
1
(
2/3
0.25 @
@ qbw % 0.047 '
(5.28)
g
((s&()Ds
Q n
((s&()Ds
where: qbw
=
unit channel width bedload transport in weight per time;
Ds
=
characteristic particle diameter;
s
=
sediment dry unit weight;
=
unit weight of water;
g
=
acceleration due to gravity;
n!
=
Manning's roughness associated with the grain resistance;
n
=
total Manning's roughness;
Q
=
water discharge; and
Qp
=
portion of discharge contributing to bedload transport.
The Meyer-Peter and Mller bedload transport equation is based on extensive laboratory flume
experiments. The range of sediment sizes used in calibration was 0.4 to 30 mm. The slope ranged from
0.0004 to 0.02.
Chien (1954) showed that the original elaborate Meyer-Peter and Mller bedload equation can
be modified to give the following relationship:
3/2
4
& 0.188
N'
(5.29)
R
where and are parameters from Einstein (1942). These parameters are stated as follows:
qbf
1
N'
(5.30a)
(s
3
(G&1)gDs
Ds
R ' (G&1)
(5.30b)
RSf
where: (G-1) = (s - )/;
183





 Previous Page
Previous Page
