70
w/L = 0.05
60
w/L = 0.1
w/L = 0.2
w/L = 0.3
50
w/L = 0.4
w/L = 0.5
40
30
20
10
0
0.2
0.4
0.6
0.8
1
nd
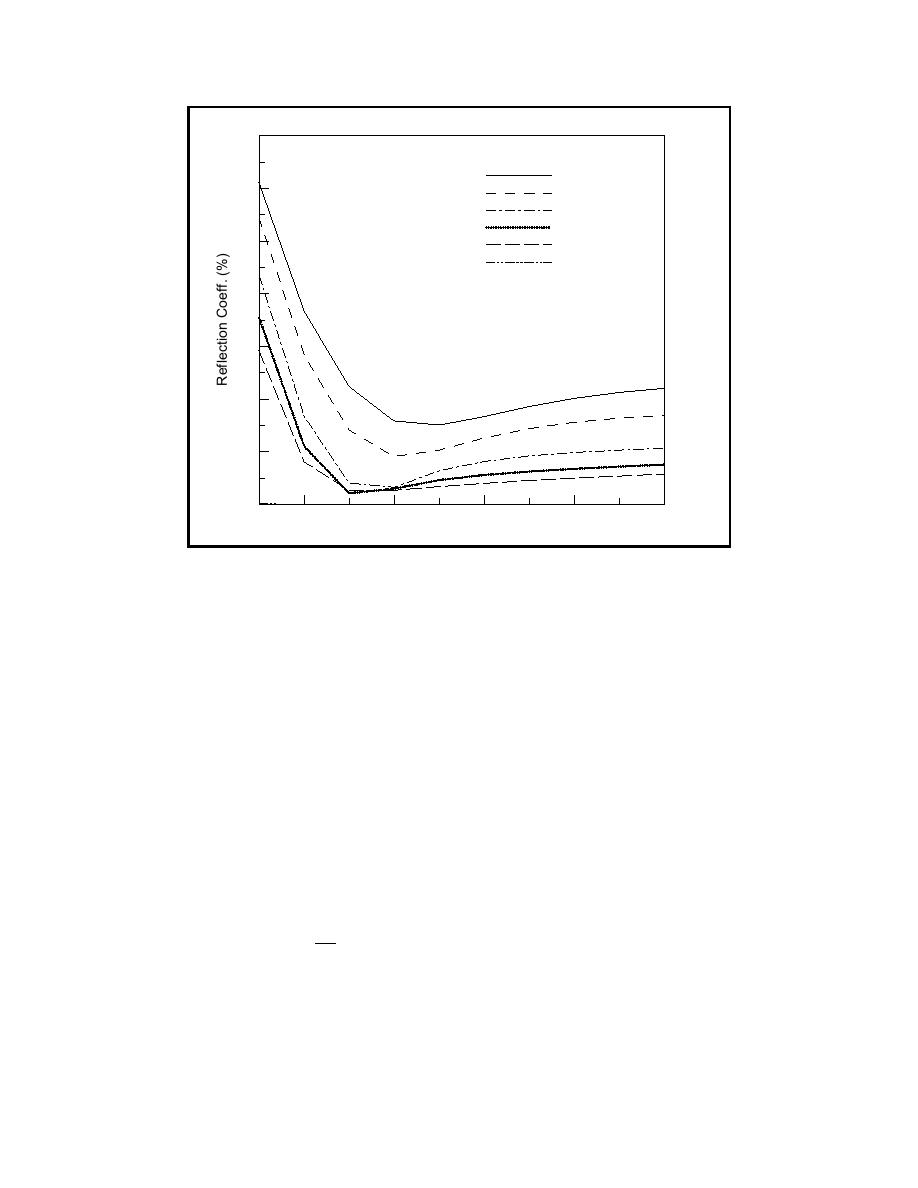
Figure 5.
Variation of reflection coefficient with damping coefficient
out that the results presented in Figure 5 are for normally incident waves. Differ-
ent reflection coefficients would be obtained for obliquely incident waves.
Flow through porous structures
The Boussinesq equations have also been modified to simulate partial wave
reflection and transmission through surface-piercing porous structures such as
breakwaters. The modified equations for the porous region can be written in
terms of either the velocity in the pores or the volume-averaged (discharge)
velocity. In order to easily match velocities and fluxes across the water/porous
structure interface, the equations for the porous region are written in terms of the
discharge velocity. Ignoring inertial effects, the modified form of the equations
for the porous region are obtained by replacing u with u/n, where n is the poros-
ity, and including a term to account for energy dissipation inside the structure:
uf
ηt + ∇ ⋅
=
(59)
0
n
24
Chapter 3 Numerical Solution





 Previous Page
Previous Page
