B.4.3. Modified Laursen Equation by Kodoatie et al. (1999)
Kodoatie adapted the Laursen methodology for analysis because this methodology was
expressed in terms which are generally recognized as important variables related to bed-
material transport. Dimensionless unit stream power was used with regression analysis and
nonlinear optimization techniques to improve the Laursen Equation. The modified Laursen
equation resulting is (variables are defined in Section 4.9):
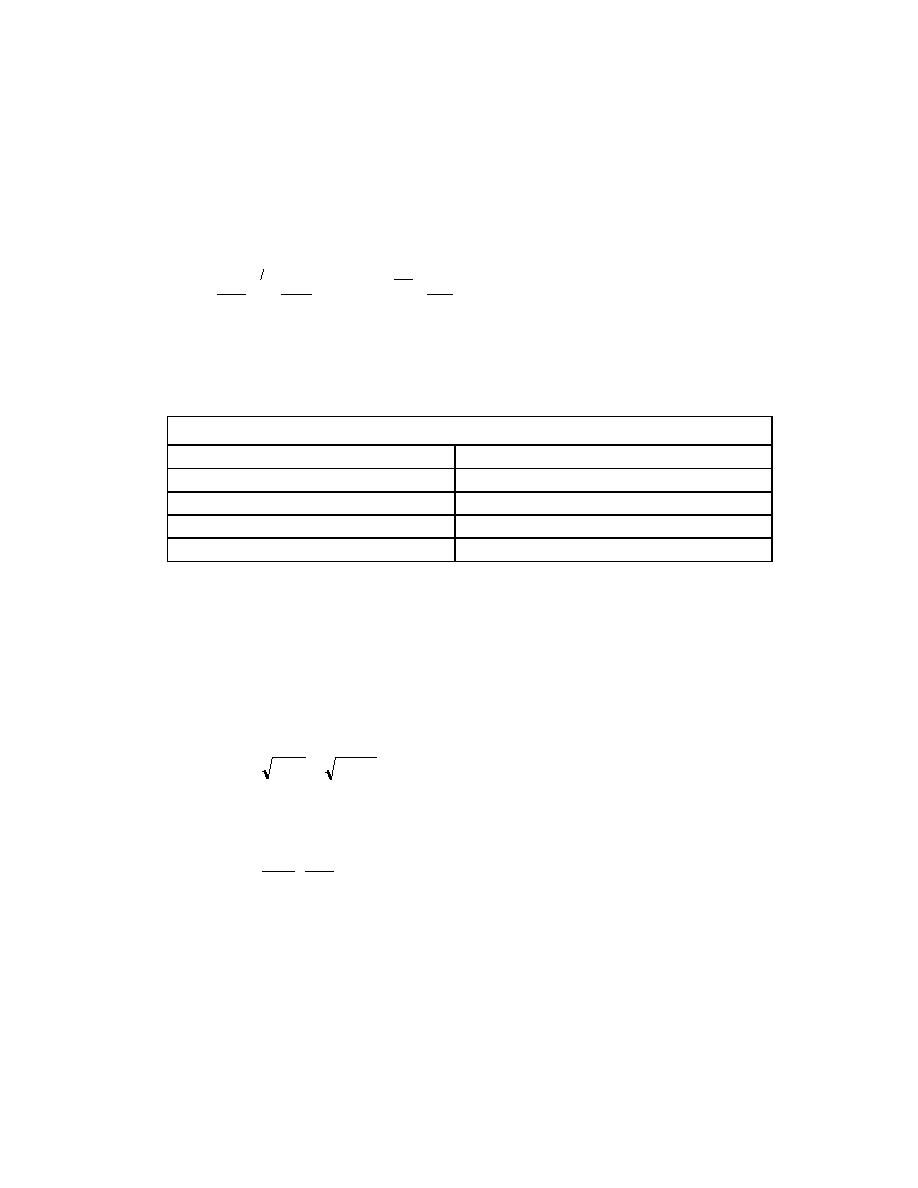
V
76
a
log f *
τo '
D
VS
ω
- 110
C t = 0.01γ 50
50
(B.10)
d
τ
ω
c50
where the coefficient a is a variable related to mean bed material diameter as shown in Table
B.11.
Table B.11. Value of "a" in Equation B.10 for Various Sizes of Bed Material.
Bed Material
"a"
Gravel
0.0
Medium to very coarse sand
-0.2
Very fine to fine sand
0.078
Silt
0.06
In equations B.7 and B.10
Sediment concentration, N/m3 (lb/ft3)
=
Ct
Unit weight of water, N/m3 (lb/ft3)
γ
=
=
Fraction by weight of bed sediment mean size, Di
pi
Di
=
Bed sediment size with I percent finer, m (ft)
y
=
Mean flow depth, m (ft)
V
=
Mean veolcity, m/s (ft/s)
=
V*
gRS = τ′ / ρ ,m / s (ft / s)
o
ω
=
Particle fall velocity, m/s (ft/s)
S
=
Slope
a
=
Exponent given in Table B.11
τo′
=
1/ 3
ρV 2
D50
2
2
y , N / m (lb / ft )
58
Particle critical shear stress = ks (γs - γ) Di, N/m2 (lb/ft2)
τci
=
=
Shields parameter
ks
Unit weight of sediment, N/m3 (lb/ft3)
γs
=
Note that in the modified Laursen equation an exponent equal to log f(V*/ω50) is a significant
variable. This parameter can be determined referring to Figure B.8. Comparison of
modifications to the Laursen equation by Madden, Copeland, and Kodoatie et al. are
presented in Table B.12.
B.24





 Previous Page
Previous Page
