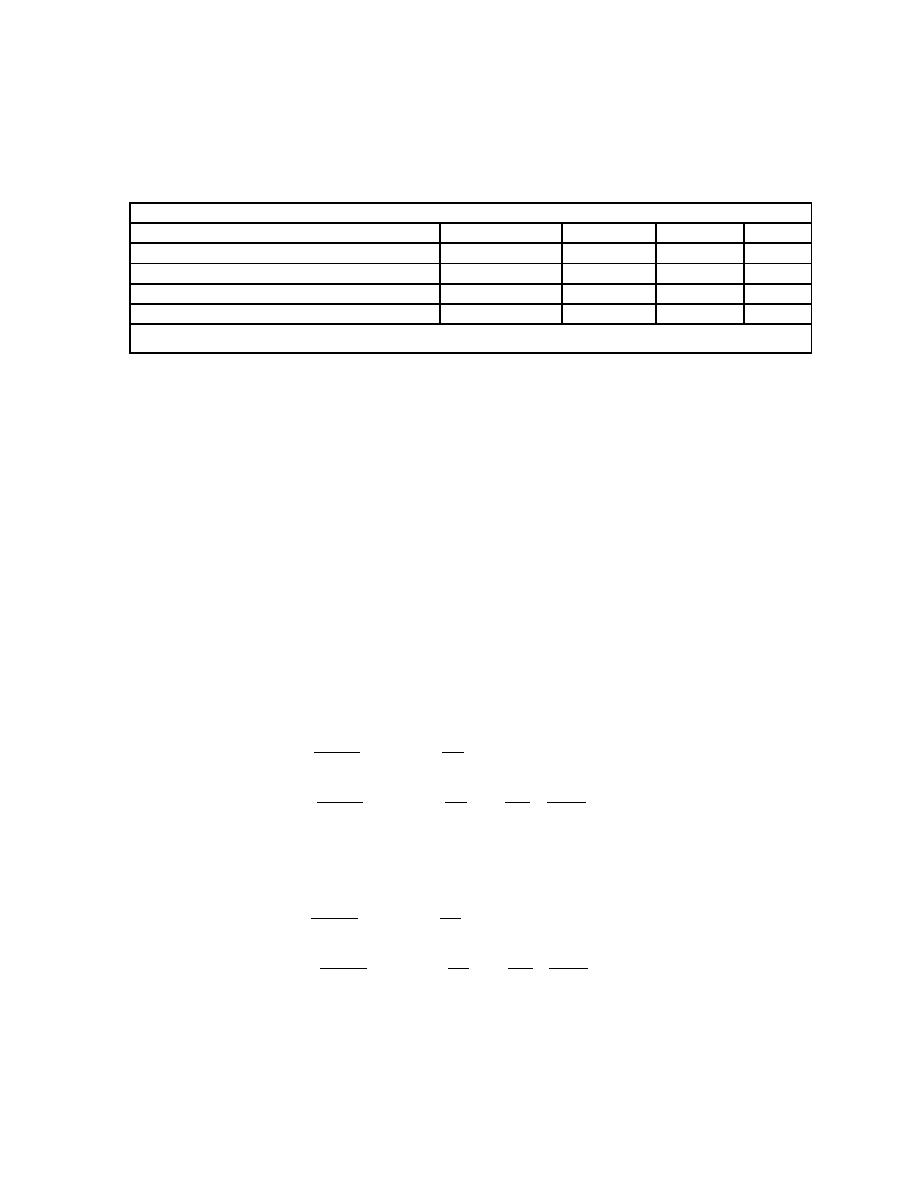
A summary of coefficient and exponents (for SI units) is presented in Table 4.3, depending
on size of bed material. Note that the values of "a" must be multiplied by a factor of 1.1
x 0.3048(1+b+c) for input and results in English units.
Table 4.3. Coefficient and Exponents for Equation 4.50.
a*
b
c
d
Silt-bed rivers
281.4
2.622
0.182
0
Very fine to fine-bed rivers
2,829.6
3.646
0.406
0.412
Medium to very coarse sand-bed rivers
2,123.4
3.300
0.468
0.613
Gravel-bed rivers
431,884.8
1.000
1.000
2.000
*a (English Units) = 1.1 x 0.3048(1+b+c) (a)
An example of the application of the expanded power function relationship is given in Section
4.12 (SI) and 4.13 (English)
4.7 YANG'S EQUATIONS
The Yang sand and gravel total load equations are presented because of their frequent
application and wide acceptance. The Yang equations are also readily adaptable to
computer solutions. Yang (1996) related total load to excess unit stream power, expressed
as the product of velocity and slope. Separate equations were developed for sand and
gravel bed material and solved for sediment concentration in ppm by weight. The regression
equations are developed based on dimensionless combinations of unit stream power, critical
unit stream power, shear velocity, fall velocity, kinematic viscosity and sediment size. Yang
also developed critical velocity formulas for use with his equations. The total load equations
can be used to compute sediment transport by size fraction by using the geometric mean of
the size class and weighting the computed concentrations by the class interval. The sand
equation, which should be used for median sizes less than 2.0 mm, is:
ωD50
V*
log C t = 5.435 - 0.286 log
- 0.457 log
ν
ω
ωD50
V VS Vcr S
- 0.314 log * log
+ 1.799 - 0.409 log
-
(4.51)
ω ω
ω
ν
and the gravel equation, which should be limited to median sizes between 2.0 and 10.0 mm,
is:
ωD50
V
- 4.816 log *
log C t = 6.681 - 0.633 log
ν
ω
ωD50
V*
VS Vcr S
+ 2.784 - 0.305 log
- 0.282 log log
-
(4.52)
ω
ω
ω
ν
4.30





 Previous Page
Previous Page
