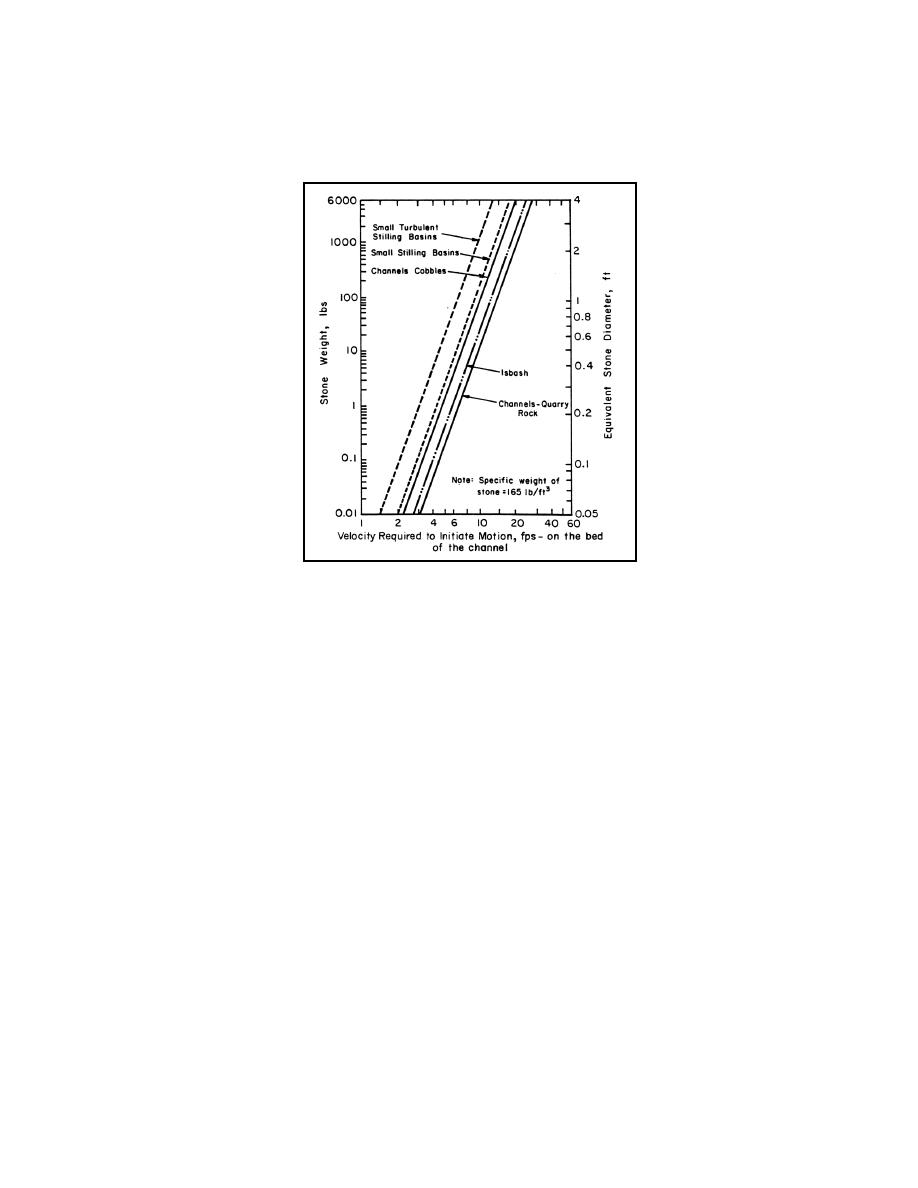
Figure 3.19 gives the relationship between maximum allowable velocity (critical velocity)
against stone or minimum stone size that can sustain hydraulic forces without motion.
Figure 3.19. Critical velocity as a function of stone size.
3.5.8 Summary
Equations 3.45 and 3.46 determine critical velocity. These equations can be used to
determine the critical size, and critical depth for the beginning of bed material movement
based on the Manning equation, specific gravity of the bed material and Shield's parameter
in metric and English units, respectively. They are for steady, uniform flow. In addition,
Equation 3.52 determines the depth of flow as a function of discharge in metric and English
units for these same conditions. To solve the equations Manning's n, specific gravity, and
Shield's parameter must be determined as well as the other variables.
In these basic equations, reasonable values of Manning's n, specific gravity, and Shield's
parameter are substituted to obtain equations for the dependent variables. These values are
(1) Shield's parameter Ks = 0.039, (2) specific gravity Ss = 2 .65, and (3) Manning's n = 0.041
D1/ 6 for metric units and n = 0.0336 D1/ 6 for English units. The derivations are given in
s
s
sufficient detail that engineers can substitute other values for Ks, Ss, and Manning's n to fit
their specific data.
Note that the critical sediment size, DC, is a function of V3 and the critical depth, y, is a
function of V6 and Q6/7.
3.45





 Previous Page
Previous Page
