from which
2Vc2
2
yc = H =
(2.147)
3
2g
or
Vc = gy c
(2.148)
Thus for maximum discharge at constant H, the Froude number is 1.0, and the flow is critical.
From this:
1/ 3
2Vc2 qmax
2
2
=
yc = H =
(see Equation 2.140)
(2.149)
g
3
2g
For critical conditions, the Froude number is 1.0, the discharge is a maximum for a given specific
head and the specific head is a minimum for a given discharge.
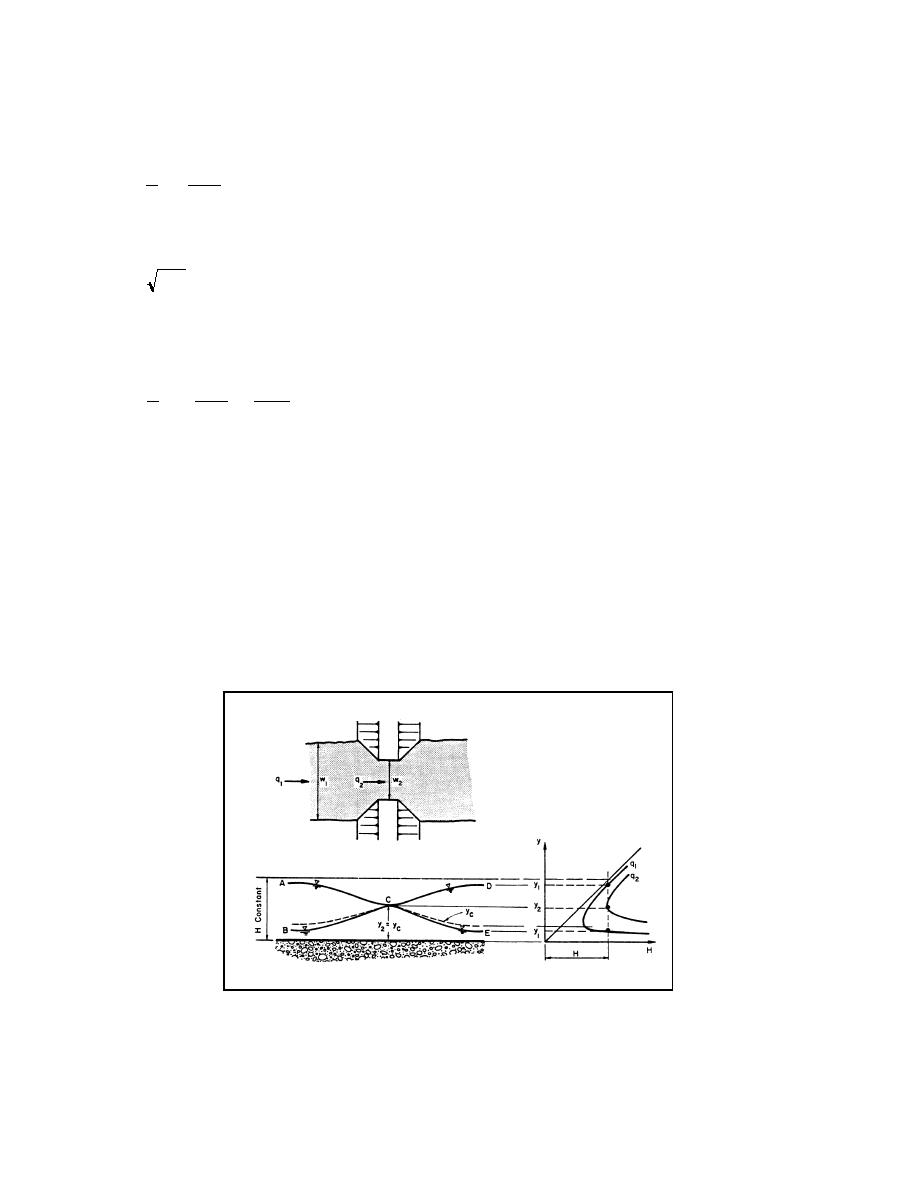
Flow conditions for constant specific head for a width contraction are illustrated in Figure 2.23
assuming a fixed bed and no geometrical effects such as eccentricity, skew, piers, and
expansion. The contraction causes a decrease in flow depth when the flow is tranquil and an
increase when the flow is rapid. The maximum possible contraction without causing backwater
effects occurs when the Froude number is one, the discharge per foot of width q is a maximum,
and yc is 2H/3. A further decrease in width will cause backwater. That is, an increase in depth
upstream will occur to produce a larger specific energy and increase yc in order to get the flow
through the decreased width.
Figure 2.23. Change in water surface elevation resulting from a change in width.
2.42





 Previous Page
Previous Page
