V
Fr =
(2.124)
gy o
When Fr < 1 (subcritical or tranquil), a small amplitude wave moves upstream. When Fr > 1
(supercritical or rapid flow), a small amplitude wave moves downstream and when Fr = 1 (critical
flow), a small amplitude wave is stationary. The fact that waves or surges cannot move upstream
when the Froude number is equal to or greater than 1.0 is important to remember when
determining when the stage-discharge relation at a cross-section can be affected by downstream
conditions. The Froude number is not only the ratio of the flow velocity to the celerity of a shallow
water wave, but is also the ratio of the inertia forces to the gravity forces.
2.5.2 Surges
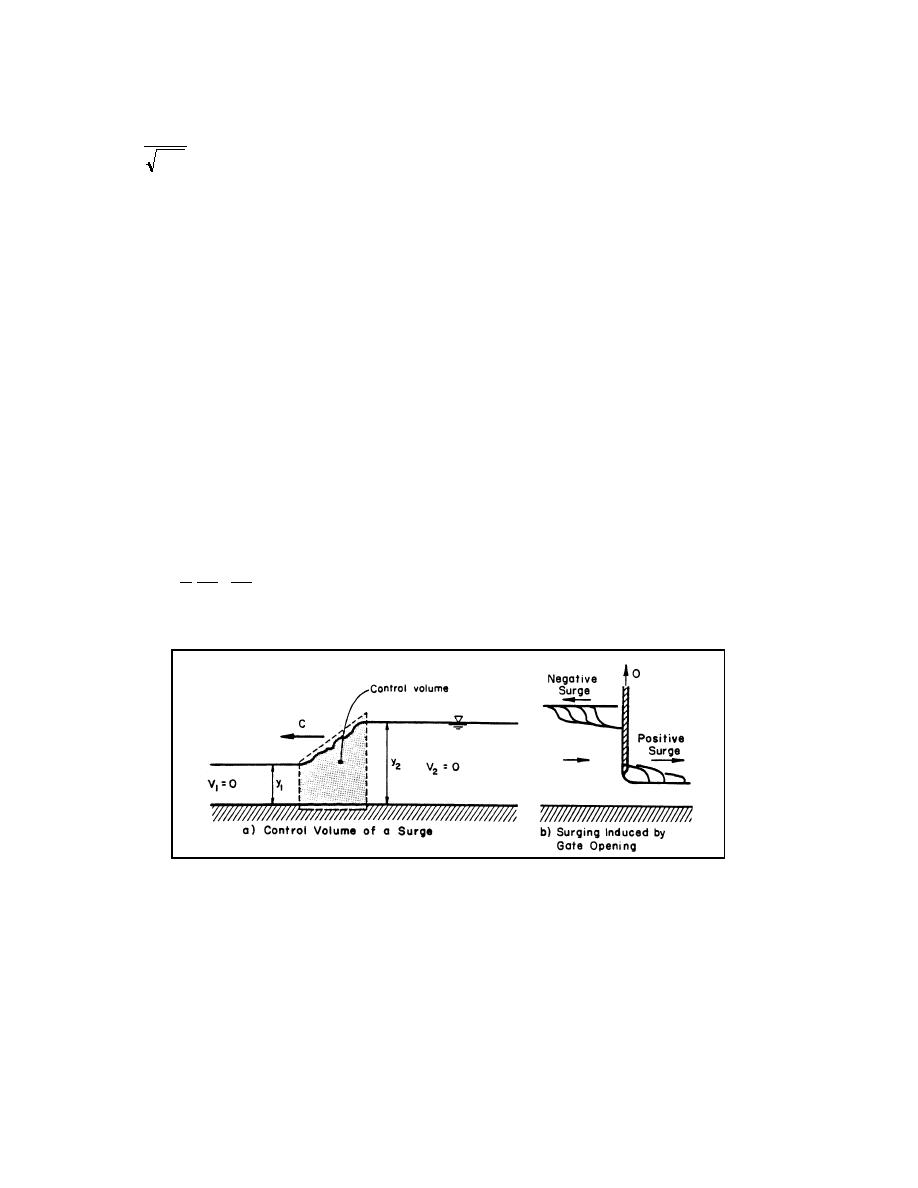
A surge is a rapid increase in the depth of flow. A surge may result from sudden release of water
from a dam, or from an incoming tide. If the ratio of wave height 2ao to the depth yo is less than
unity, the surge has an undulating wave form. If 2ao/yo is greater than one, the first wave breaks
and produces a discontinuous surface. The breaking wave dissipates energy and the previous
equations for wave celerity are invalid. However, by applying the momentum and continuity
equations for a control volume encompassing the surge shown in Figure 2.15, the equation for
the celerity of a surge can be derived for flat slopes as:
1/ 2
1 y2 y2
+ 1
c = gy 1
(2.125)
2 y1 y1
Figure 2.15. Sketch of positive and negative surges.
Equation 2.125 gives the velocity of a surge as it moves upstream as the result of a sudden total
or partial closure of gates, or of an incoming tide, or of a surge that moves downstream as the
result of a sudden opening of a gate. The lifting of a gate in a channel sketched in Figure 2.15b
not only causes a positive surge to move downstream, it also causes a negative surge to move
upstream. Equation 2.125 is approximately correct for the celerity of the negative surge if the
height of the surge is small compared to the depth. As it moves upstream a negative surge
quickly flattens out.
2.34





 Previous Page
Previous Page
